K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
21 tháng 9 2018
Đáp án: D
Điều kiện xác định của phương trình là
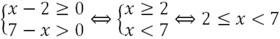
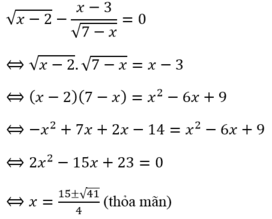
=> Tích 2 nghiệm của phương trình là
DV
3
19 tháng 5 2016
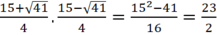
49 x (37+25) + 62 x (121- 60)
= 49 x 62 + 62 x 61
= 62 x (49+61)
=6820
19 tháng 5 2016
49*(37+25)+62*(121-60)
=49*62+62*61
=62*(49+61)
=62*110
=6820
NH
1
HH
25 tháng 6 2018
Giải:
a) Không ghi rõ đề nên mình không làm được
b) \(\left|x+1\right|< 2\)
Mà \(\left|x+1\right|\ge0\)
\(\Leftrightarrow\left|x+1\right|=\left\{0,1\right\}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+1=-1\\x+1=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\\x=0\end{matrix}\right.\)
Vậy ...
1 tháng 2 2017
Thay \(x=37;m=72\) vào \(m-24-x+24+x\) , ta có :
\(72-24-37+24+37\)
\(=\left(-24+24\right)+\left(37-37\right)+72\)
\(=0+0+72\)
\(=72\)
TC
1
14 tháng 3 2023
Ta có \(x^2+4x-5\ge0\) \(\Leftrightarrow\left(x-1\right)\left(x+5\right)\ge0\)
Đặt \(f\left(x\right)=\left(x-1\right)\left(x+5\right)\). Ta thấy \(1,-5\) là các nghiệm đơn của \(f\left(x\right)\). Ta lập bảng xét dấu:
| \(x\) | \(-\infty\) \(-5\) \(1\) \(+\infty\) |
| \(f\left(x\right)\) | \(+\) \(-\) \(0\) \(+\) |
Ta suy ra \(f\left(x\right)\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge1\\x\le-5\end{matrix}\right.\)
Vậy bất phương trình đã cho có tập nghiệm \(S=\left\{x\inℝ|\left(x\ge1\right)V\left(x\le-5\right)\right\}\)
22 tháng 3 2020
Ta có: \(13\cdot\left(-37\right)-23\cdot37-46\cdot\left(-37\right)\)
\(=13\cdot\left(-37\right)+23\cdot\left(-37\right)-46\cdot\left(-37\right)\)
\(=\left(-37\right)\cdot\left(13+23-46\right)\)
\(=\left(-37\right)\cdot\left(-10\right)=370\)
12 tháng 8 2019
1.
a) 13\(\frac{1}{3}\) : 1\(\frac{1}{3}\) = 26 : (2x - 1)
<=> \(\frac{40}{3}:\frac{4}{3}\) = 13x - 26
<=> 10 + 26 = 13x
<=> 13x = 36
<=> x = \(\frac{36}{13}\)
b) 0,2 : 1\(\frac{1}{5}\) = \(\frac{2}{3}\) : (6x + 7)
<=> \(\frac{1}{5}:\frac{6}{5}\) = \(\frac{1}{9}x\) : \(\frac{2}{21}\)
<=> \(\frac{1}{6}\) = \(\frac{1}{9}x\) : \(\frac{2}{21}\)
<=> \(\frac{1}{9}x\) = \(\frac{2}{21}.\frac{1}{6}\) = \(\frac{1}{63}\)
<=> x = \(\frac{1}{7}\)
c) \(\frac{37-x}{x+13}\) = \(\frac{3}{7}\)
<=> (37 - x) . 7 = 3.(x + 13)
<=> 119 - 7x = 3x + 39
<=> -7x - 3x = 39 - 119
<=> -10x = -80
<=> x = 8
d) \(\frac{x-1}{x+5}=\frac{6}{7}\)
<=> 7(x - 1) = 6(x + 5)
<=> 7x - 7 = 6x + 30
<=> 7x - 6x = 30 + 7
<=> x = 37
e)
2\(\frac{2}{\frac{3}{0,002}}\) = \(\frac{1\frac{1}{9}}{x}\)
<=> \(\frac{1501}{750}\) = \(\frac{10}{9}:x\)
<=> x = \(\frac{10}{9}:\frac{1501}{750}\) = \(\frac{2500}{4503}\)
12 tháng 8 2019
Bài 2. đề sai
Bài 3.
a) 6,88 : x = \(\frac{12}{27}\)
<=> x = 6,88 : \(\frac{12}{27}\)
<=> x = 15,48
b) 8\(\frac{1}{3}\) : \(11\frac{2}{3}\) = 13 : 2x
<=> \(\frac{25}{3}:\frac{35}{3}\) = 13 : 2x
<=> \(\frac{5}{7}=13:2x\)
<=> 2x = \(13:\frac{5}{7}\) = \(\frac{91}{5}\)
<=> x = 9,1
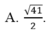
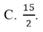
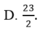
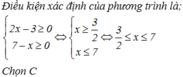
\(-37-\left|7-x\right|=-127\)
th1 : \(x\le7\) thì \(-37-\left|7-x\right|=-127\)
\(\Leftrightarrow\) \(-37-\left(7-x\right)=-127\) \(\Leftrightarrow\) \(-37-7+x=-127\)
\(\Leftrightarrow\) \(x=-127+37+7=-83\)
th2 : \(x>7\) thì \(-37-\left|7-x\right|=-127\)
\(\Leftrightarrow\) \(-37-\left(x-7\right)=-127\) \(\Leftrightarrow\) \(-37-x+7=-127\)
\(\Leftrightarrow\) \(-x=-127+37-7=-97\Leftrightarrow x=97\)
vậy \(x=-83;x=97\)