Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Answer:
a. Tam giác ABC cân tại A
=> Góc ABC = góc ACB
=> BD là tia phân giác của góc ABC
\(\Rightarrow\widehat{BDC}=\frac{\widehat{ABC}}{2}\)
CE là tia phân giác của góc ACB
\(\Rightarrow\widehat{BCE}=\frac{\widehat{ACB}}{2}\)
=> Góc BDC = góc BCE
Xét tam giác BCE và tam giác CBD:
BC cạnh chung
Góc CBE = góc BCD
Góc BCE = góc CBD
=> Tam giác BCE = tam giác CBD (g.c.g)
=> BD = CE
b. Có: \(\frac{BE}{AB}=\frac{DC}{AC}\Rightarrow ED//BC\)
c. Có: \(\frac{AD}{DC}=\frac{AB}{BC}\)
\(\Rightarrow\frac{AD}{DC}=\frac{6}{4}=\frac{3}{2}\)
\(\Rightarrow AD=\frac{3}{2}DC\)
Mà AD + DC = AC
\(\frac{3}{2}DC+DC=6\)
\(\Rightarrow DC=2,4cm\)
\(\Rightarrow AD=3,6cm\)
Có \(\frac{ED}{BC}=\frac{AD}{AC}\)
\(\Rightarrow ED=\frac{BC.AD}{AC}=\frac{4.3,6}{6}=2,4cm\)

- Vì tam giác \(\Delta ABC\)cân tại A Nên : \(\widehat{ABC}=\widehat{ACB}\)mà BD,CE lần lượt là đường phân giác của hai góc \(\widehat{ABD};\widehat{ACD}\Rightarrow\widehat{ABD}=\widehat{ACE}\)\(\Rightarrow\hept{\begin{cases}\widehat{BAC}chung\\AB=AC\\\widehat{ABD}=\widehat{ACE}\end{cases}}\Rightarrow\Delta ABD=\Delta ACE\Rightarrow BD=CE\)
- \(\Delta ABD=\Delta ACE\Rightarrow AE=AD\Rightarrow\frac{AE}{AB}=\frac{AD}{AC}\)\(\Rightarrow ED||BC\)
- Gọi độ dài của AD là \(x\left(cm\right)\)\(\Rightarrow DC=6-x\left(cm\right)\)vì BD là phân giác của \(\widehat{ABD}\)nên có tỉ số : \(\frac{AD}{DC}=\frac{AB}{BC}\Leftrightarrow\frac{x}{6-x}=\frac{6}{4}\Leftrightarrow10x=36\Leftrightarrow x=3,6\left(cm\right)\)\(\Rightarrow DC=6-3,6=2,4\left(cm\right)\)mặt khác từ tỉ số : \(\frac{ED}{BC}=\frac{AD}{AC}\Rightarrow ED=\frac{AD.BC}{AC}=\frac{3,6.4}{6}=2,4\left(cm\right)\)

a) Xét tam giác BEC và tam giác CDB có:
góc ABC = góc ACB (tam giác ABC cân tại A);
BC chung;
góc ECB = góc DBC \(\left(=\dfrac{\widehat{ABC}}{2}=\dfrac{\widehat{ACB}}{2}\right)\)
=> tam giác BEC = tam giác CDB (g-c-g)
=> EC = DB (2 cạnh tương ứng)
b) theo câu a) ta có tam giác EBC = tam giác DCB (g-c-g)
=> BE = DC (2 cạnh tương ứng)
=> AE = AD (=AB-BE=AC-DC)
=> tam giác AED cân tại A
=> góc AED = (1800 - góc BAC):2 (*)
cũng như trong tam giác ABC cân tại A thì
góc ABC = (1800 - góc BAC):2 (**)
Từ (*)(**)=> góc AED = góc ABC (ở vị trí đồng vị)
=> ED song song với BC
c) Theo tính chất đường phân giác trong tam giác thì ta có:
\(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Leftrightarrow\dfrac{AB}{AD}=\dfrac{BC}{DC}\Leftrightarrow\dfrac{AB+BC}{AD+DC}\)
\(\Leftrightarrow\dfrac{AB+BC}{AC}=\dfrac{6+4}{6}=\dfrac{10}{6}=\dfrac{5}{3}\)
\(\Rightarrow AD=AB:\dfrac{5}{3}=6:\dfrac{5}{3}=\dfrac{18}{5}=3,6\left(cm\right)\)
và \(DC=AC-AD=6-3,6=2,4\left(cm\right)\)
Mặt khác:\(\dfrac{AD}{AC}=\dfrac{ED}{BC}\Rightarrow ED=\dfrac{AD.BC}{AC}=\dfrac{3,6.4}{6}=2,4\left(cm\right)\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{AC}{16}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{CD}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\CD=5\left(cm\right)\end{matrix}\right.\)
Vậy: BC=10cm; AD=3cm; CD=5cm
b) Ta có: \(\dfrac{CE}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)
\(\dfrac{CD}{CB}=\dfrac{5}{10}=\dfrac{1}{2}\)
Do đó: \(\dfrac{CE}{CA}=\dfrac{CD}{CB}\)
Xét ΔCED và ΔCAB có
\(\dfrac{CE}{CA}=\dfrac{CD}{CB}\)(cmt)
\(\widehat{C}\) chung
Do đó: ΔCED\(\sim\)ΔCAB(c-g-c)

a) áp dụng định lí pitago vào tam giác abc được ab2 +ac2=bc2 suy ra bc2= 32+42=25 suy ra bc=5
có bd là phân giác góc abc nên ab/ad=bc/dc
dùng tính chất dãy tỉ số bằng nhau ta có ab/ad=bc/dc=(ab+bc)/(ad+dc)=(3+5)/4=2
nên ad=ab/2=3/2
dc=bc/2=5/2
b) dựa vào số đo độ đài cm được ec/ac=dc/bc
xét tam giác abc vuông và tam giác edc vuông có góc c chung và ea/ac=dc/bc nên suy ra 2 tam giác đó đồng dạng
c) tg abc và tg edc đồng dạng suy ra de vuông góc với bc
bd là phân giác abc có de vuông góc với bc, da vuông góc với ab nên suy ra de=da (tính châts này đã học ở lớp 7)
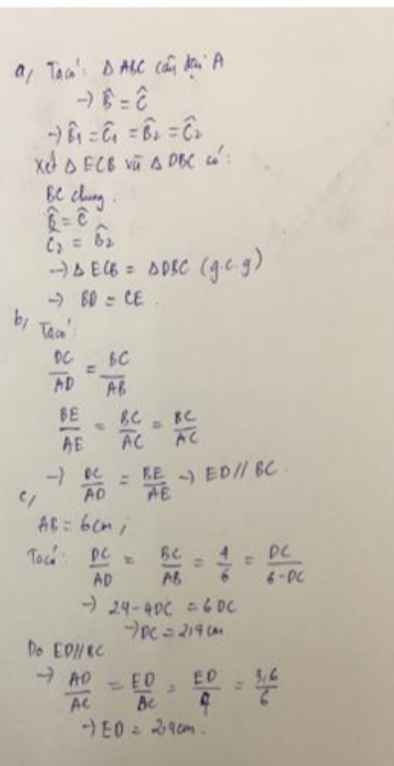

câu a
tam giác abc có ab = ac
=> tam giác abc cân tại a
=> góc b = góc c
=> góc b1 = góc c1 (phân giác 2 góc = nhau)
tam giácc bcd và tam giác cbe có
chung bc
góc b = góc c
góc b1 = góc c1
=> tam giác bcd = tam giác cbe (gcg)
=> bd = ce
câu b
câu a
\(\)=> cd = be
có ab = ac
\(=>\dfrac{cd}{ac}=\dfrac{be}{ab}\\ \)
=> ed // bc (ta lét đảo)
câu c
tam giác abc có bd là phân giác góc b
\(=>\dfrac{ab}{bc}=\dfrac{ad}{cd}\\ =>\dfrac{ab}{bc+ab}=\dfrac{ad}{ad+cd}\\ =>\dfrac{ab}{bc+ab}=\dfrac{ad}{ac}\\ =>\dfrac{6}{6+4}=\dfrac{ad}{6}\\ =>\dfrac{6}{10}=\dfrac{ad}{6}\\ =>ad=3,6\left(cm\right)\)
có ad +cd = ac
=> 3,6 + cd = 6
=> cd = 2,4 (cm)
có ed // bc
\(=>\dfrac{ed}{bc}=\dfrac{ad}{ac}\\ =>\dfrac{ed}{4}=\dfrac{3,6}{6}\\ =>ed=2,4\left(cm\right)\)
thế thoi, chúc may mắn :)