
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


N=(22-12)+(42-32)+(62-52)+....+(1002-992)
=(2-1)(2+1)+(4-3)(4+3)+....+(100-99)(100+99)
=3+7+11+15+....+195+199=(199+3)(\(\dfrac{199-3}{4}\)+1)=10100



A=2+2^2+2^3+...+2^59+2^60(có 60 số hạng)
A=(2+2^2+2^3)+(2^4+2^5+2^6)+...+(2^58+2^59+2^60)[có 20 nhóm]
A=14*1+2^3*(2+2^2+2^3)+...+2^57*(2+2^2+2^3)
A=14*1+2^3*14+...+2^57*14
A=14*(1+2^3+...+2^57)
A=7*2*(1+2^3+...+2^57) chia hết cho 7(tick nha![]() )
)

Ta có S=\(\frac{1+2+2^2+...+2^{2015}}{1-2^{2016}}\)
Đặt M là tử của 2 ta có
M=1+2+2^2+...+2^2015
2M=2*(1+2+2^2+...+2^2015)
2M=2+2^2+2^3+...+2^2016
2M-M=(2+2^2+2^3+...+2^2016)-(1+2+2^2+...+2^2015)
M=2^2016-1
S=\(\frac{2^{2016}-1}{1-2^{2016}}\)
Ta thấy tử và mẫu của S là 2 số đối nhau.Mà 2 số đối nhau luôn có thương là -1
Nên S=-1

\(S=\frac{1}{2^2}-\frac{1}{2^4}+\frac{1}{2^6}-....+\frac{1}{2^{4n-2}}-\frac{1}{2^{4n}}+...+\frac{1}{2^{2002}}-\frac{1}{2^{2004}}\)
\(<\frac{1}{2^4}-\frac{1}{2^4}+\frac{1}{2^8}-\frac{1}{2^8}+...+\frac{1}{2^{4n}}-\frac{1}{2^{4n}}+...+\frac{1}{2^{2004}}-\frac{1}{2^{2004}}\)=0+0+0+...+0+....+0=0 <0,2
Vậy S<0,2

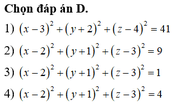
2 - 2 = 0