Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1: (Sgk/36):
a. \(\dfrac{5y}{7}\)=\(\dfrac{20xy}{28x}\) vì
5y . 28x = 140xy
7 . 20xy = 140xy
=> 5y . 28x = 7 . 20xy
Vậy \(\dfrac{5y}{7}\)=\(\dfrac{20xy}{28x}\)
b. \(\dfrac{3x\left(x+5\right)}{2\left(x+5\right)}\)=\(\dfrac{3x}{2}\) vì
3x . 2(x+5) = 6x2+30x
2 . 3x(x+5) = 6x2+30x
=> 3x . 2(x+5) = 2 . 3x(x+5)
Vậy \(\dfrac{3x\left(x+5\right)}{2\left(x+5\right)}\)=\(\dfrac{3x}{2}\)
c. \(\dfrac{x+2}{x-1}\)=\(\dfrac{\left(x+2\right)\left(x+1\right)}{x^2-1}\) vì
(x+2) (x2-1) = (x+2) (x-1) (x-1)
=> (x+2) (x2-1) = (x-1) (x+2) (x+1)
Vậy \(\dfrac{x+2}{x-1}\)=\(\dfrac{\left(x+2\right)\left(x+1\right)}{x^2-1}\)
d. \(\dfrac{x^2-x-2}{x+1}\)=\(\dfrac{x^2-3x+2}{x-1}\)
(x-1) (x2-x-2) = x3-2x2-x+2
(x+1) (x2-3x+2) = x3-2x2-x+2
=> (x-1) (x2-x-2) = (x2-3x+2) (x+1)
Vậy \(\dfrac{x^2-x-2}{x+1}\)=\(\dfrac{x^2-3x+2}{x-1}\)

Xin được mạn phép chữa đề.
\(\text{c) }\dfrac{x+2}{x+1}=\dfrac{\left(x+2\right)\left(x-1\right)}{x^2-1}\)
\(\text{Ta có : }\dfrac{\left(x+2\right)\left(x-1\right)}{x^2-1}=\dfrac{\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+2}{x+1}\left(đpcm\right)\)
Vậy.......................
c) x+2x+1=(x+2)(x−1)x2−1c) x+2x+1=(x+2)(x−1)x2−1
Ta có : (x+2)(x−1)x2−1=(x+2)(x−1)(x−1)(x+1)=x+2x+1(đpcm)
Vậy

Ta có:
(x+y).9x2.(x+y)=9x2.(x+y)2
3x.3x.(x+y)2=9x2.(x+y)2
=>(x+y).9x2.(x+y)=3x.3x.(x+y)2
=>\(\dfrac{x+y}{3x}=\dfrac{3x\left(x+y\right)^2}{9x^2.\left(x+y\right)}\)
Cách khác :
Ta có :
\(\dfrac{3x\left(x+y\right)^2}{9x^2\left(x+y\right)}=\dfrac{x+y}{3x}\)
Do : \(\dfrac{x+y}{3x}=\dfrac{x+y}{3x}\)
Nên...................

a ) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\) (1)
\(\dfrac{2x^2+x-1}{6x-3}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\) (2)
Từ (1) ; (2) \(\Rightarrow\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) (đpcm)
b ) \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\) (3)
\(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\) (4)
Từ (3) và (4) \(\Rightarrow\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\) (đpcm)
a) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{x^2+x+2x+2}{3\left(x+2\right)}=\dfrac{\left(x^2+x\right)+\left(2x+2\right)}{3\left(x+2\right)}=\dfrac{x\left(x+1\right)+2\left(x+1\right)}{3\left(x+2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\left(1\right)\) \(\dfrac{2x^2+x-1}{6x-3}=\dfrac{2x^2+2x-x-1}{3\left(2x-1\right)}=\dfrac{2x\left(x+1\right)-\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\left(2\right)\) Từ (1)và (2)=> \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) b)\(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{3x\left(x+1\right)-2\left(x+1\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\left(3\right)\) \(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\left(4\right)\) Từ (3) và (4) => \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\)

Ta có: \(\dfrac{x^3+8}{x^2-2x+4}=x+2\)
\(\Rightarrow\left(x^3+8\right)=\left(x^2-2.x+2^2\right)\left(x+2\right)\)
\(\Rightarrow x^3+8=x^3+8\)
\(\rightarrowđpcm.\)

a) Ta có:
\(\begin{array}{l}3{\rm{x}}.10y = 30{\rm{xy}}\\{\rm{2}}{\rm{.15x}}y = 30{\rm{x}}y\end{array}\)
Suy ra: \(3{\rm{x}}.10 = 2.15{\rm{x}}y\) nên \(\dfrac{{3{\rm{x}}}}{2} = \dfrac{{15{\rm{x}}y}}{{10y}}\)
b) Ta có:
\(\begin{array}{l}\left( {3{\rm{x}} - 3y} \right).2 = 2.3\left( {x - y} \right) = 6\left( {x - y} \right)\\\left( { - 3} \right).\left( {2y - 2{\rm{x}}} \right) = \left( { - 3} \right).\left( { - 2} \right)\left( {x - y} \right) = 6\left( {x - y} \right)\end{array}\)
Suy ra: \(2.\left( {3{\rm{x}} - 3y} \right) = \left( { - 3} \right).\left( {2y - 2{\rm{x}}} \right)\) nên \(\dfrac{{3{\rm{x}} - 3y}}{{2y - 2{\rm{x}}}} = \dfrac{{ - 3}}{2}\)
c) Ta có: \(\begin{array}{l}\left( {{x^2} - x + 1} \right).x\left( {x + 1} \right) = x.\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = x.\left( {{x^3} + 1} \right)\\x.\left( {{x^3} + 1} \right)\end{array}\)
Suy ra: \(\left( {{x^2} - x + 1} \right).x.\left( {x + 1} \right) = x.\left( {{x^3} + 1} \right)\) nên \(\dfrac{{{x^2} - x + 1}}{x} = \dfrac{{{x^3} + 1}}{{x\left( {x + 1} \right)}}\)
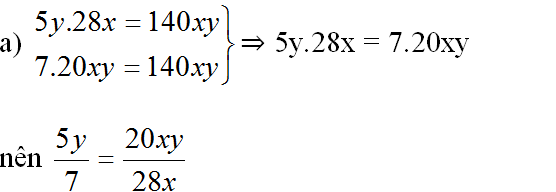

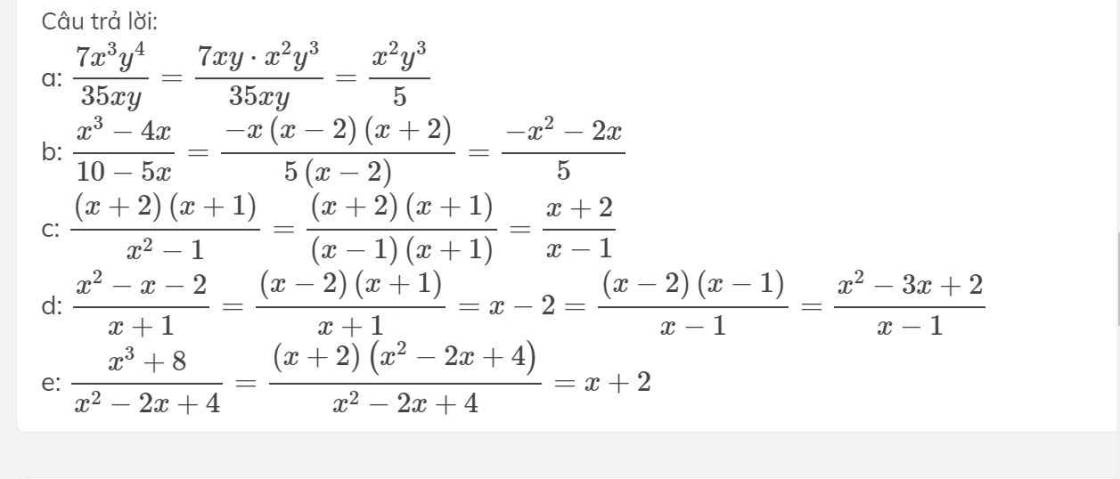
pt <=> \(\left(x^2-x-2\right)\left(x-1\right)=\left(x+1\right)\left(x^2-3x+2\right)\)
\(\Leftrightarrow\left(x^2+x-2x-2\right)\left(x-1\right)=\left(x+1\right)\left(x^2-x-2x+2\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\left(x-1\right)=\left(x+1\right)\left(x-2\right)\left(x-1\right)\)(Đúng \(\forall x\) )
Ta có:
\(\left(x^2-x-2\right)\left(x-1\right)\)
= \(\left(x^2-2x+x-2\right)\left(x-1\right)\)
= \([\left(x^2-2x)+(x-2\right)]\left(x-1\right)\)
= \([x\left(x-2)+(x-2\right)]\left(x-1\right)\)
= \(\left(x-2\right)\left(x+1\right)\left(x-1\right)\) (1)
Lại có:
\((x^2-3x+2)\left(x+1\right)\)
= \((x^2-2x-x+2)\left(x+1\right)\)
= \([(x^2-2x)-(x-2)]\left(x+1\right)\)
= \([x(x-2)-(x-2)]\left(x+1\right)\)
= \(\left(x-2\right)\left(x-1\right)\left(x+1\right)\) (2)
Từ (1), (2)
=> \(\left(x^2-x-2\right)\left(x-1\right)\) = \((x^2-3x+2)\left(x+1\right)\)
=> \(\dfrac{x^2-x-2}{x+1}=\dfrac{x^2-3x+2}{x-1}\)