
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giữa vân sáng bậc 3 và bậc 9 bức xạ $\lambda _{1}$ có số vân sáng của bức xạ $\lambda _{1}$ :
3 < k1 < 9 $\Rightarrow $ có 5 vân sáng
Giữa vân bậc 3 và 9 của bức xạ $\lambda _{1}$ có số vân sáng của bức xạ $\lambda _{2}$:
$\dfrac{3.\lambda_1}{\lambda_2}$ < k2 < $\dfrac{9.\lambda_1}{\lambda_2}$
$\Leftrightarrow $ 4 < k2 < 12 suy ra k2= 7
Mà giữa vân bậc 3 và 9 của bức xạ $\lambda _{1}$ có 1 vị trí vân sáng bức xạ $\lambda _{1}$ và $\lambda _{2}$ trùng nhau (tại vân sáng thứ 6) nên số vân sáng sẽ là : 7 + 5 - 1 = 11 vân sáng

Khối lượng còn lại của hai đồng vị sau thời gian t là
\(m(238) = m_{0238}.2^{-t/T_1}.\\ m(235) = m_{0235}.2^{-t/T_2}.\)
Chi hai phương trình ta thu được
\(\frac{m(238)}{m(235)} = 2^{t(\frac{1}{T_2}-\frac{1}{T_1})}.(2)\)
mà hiện tại tỉ số khối lượng của chúng là \(\frac{92,848}{7,142} = 13.\)
Thay vào phương trình (2) ta được \(2^{t(1/T_2-1/T_1)} = 13 => t (1/T_2-1/T_1) = \ln_2{13} => t \approx 3,1.10^9\) năm.
Vậy tuổi Trái Đất cỡ 3,1 tỷ năm.

Ta có: \(P=UI\cos\left(\varphi_u-\varphi_1\right)=100.2.\cos\left(-\frac{\pi}{3}\right)=100\left(W\right)\)
Đáp án D.

Đáp án C
Phương pháp: Áp dụng công thức tính chu kì dao động của con lắc đơn
Cách giải:
Chu kì dao động của con lắc sau khi bị vướng vào đinh gồm:
+ ½ chu kì dao động với chiều dài dây l
+ ½ chu kì dao động với chiều dài dây l’ = 4l/9
Chu kì dao động của con lắc có chiều dài l: T 0 = 2 π l g
Chu kì dao động của con lắc với chiều dài dây 4l/9 là: T ' = 2 π l g
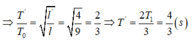
=> Chu kì dao động mới của con lắc vướng đinh là: T = (T’+ T0)/2 = 1,67s
=> Chọn C

Đáp án C
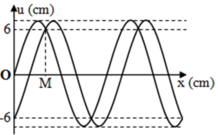
Gọi điểm đầu sợi dây là O.
Tại t1: O đang ở VTCB và đi xuống, M ở li độ +6 cm và đi lên.
Tại t2: O đang ở li độ −6 cm và đi xuống, M ở li độ +6 cm và đi xuống.
Dựa vào vòng tròn lượng giác ta tính được: T = 1 9 : 1 6 = 2 3 s
Tại t3 thì v M = 3 π . ( 4 3 ) 2 - 0 , 9 2 ≈ 64 , 74 cm
0,1111111111
Đáp Án :
1:9=1/9
#Kuân08