Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tốc độ điểm nằm trên vành: v1=wR
Tốc độ điểm nằm chính giữa vành và tâm: v2=w\(\dfrac{R}{2}\)
\(\Rightarrow\) Tỉ số \(\dfrac{v_1}{v_2}\)= 2

Theo công thức của chuyển động quay biến đổi đều
\(\omega^2-\omega^2_0=2.\gamma.\varphi\)
\(\left(\omega-\omega_0\right).\left(\omega+\omega_0\right)=2.\frac{\left(\omega-\omega_0\right)}{t}.\varphi\)
\(\left(\omega+\omega_0\right).t=2.\varphi\)
Với \(t=30s\), \(\omega=20\pi\) và \(\varphi=360\pi\)
suy ra
\(\omega_0=4.\pi\) rad/s và \(\gamma=16\pi\text{ /}30\) rad/s2
Thời gian để đạt được tốc độ \(\omega_0\) từ trạng thái nghỉ là \(\omega_0\text{π /}\gamma\) = 7.5 s
Phương trình chuyển động của bánh xe từ trạng thái nghỉ là
\(\varphi\)= (1/2 ). (16\(\pi\)/30).t2 rad

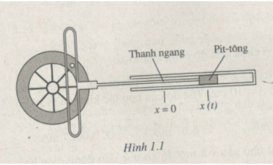
Thanh ngang trùng với trục Ox. Hình chiều của quả cầu trên trục Ox trùng với đầu thanh ngang. Do đó khi quả cầu chuyển động tròn đều thì thanh ngang và pít - tông dao động điều hòa

B. momen quán tính của người giảm, tốc độ góc trong chuyển động quay của người tăng.

C. gia tốc góc của bánh xe có độ lớn tăng lên