K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 10 2021
3: \(\left(x+5\right)\left(x^2-5x+25\right)-x\left(x-4\right)^2+16x\)
\(=x^3+125-x^3+8x^2-16x+16x\)
\(=8x^2+125\)
CM
3 tháng 3 2018
Ta có
(A):
16 x 4 ( x – y ) – x + y = 16 x 4 ( x – y ) – ( x – y ) = ( 16 x 4 – 1 ) ( x – y ) = [ ( 2 x ) 4 – 1 ] ( x – y ) = [ ( 2 x ) 2 – 1 ] [ ( 2 x ) 2 + 1 ] ( x – y ) = ( 2 x – 1 ) ( 2 x + 1 ) ( 4 x 2 + 1 ) ( x – y )
Nên (A) sai
Và (B):
2 x 3 y – 2 x y 3 – 4 x y 2 – 2 x y = 2 x y ( x 2 – y 2 – 2 y – 1 ) = 2 x y [ x 2 – ( y 2 + 2 y + 1 ) ] = 2 x y [ x 2 – ( y + 1 ) 2 ] = 2 x y ( x – y – 1 ) ( x + y + 1 ) .
Nên (B) sai.
Vậy cả (A) và (B) đều sai.
Đáp án cần chọn là: C
18 tháng 7 2021
`(2x-y)(16x^4+8x^3y+4x^2y^2+2xy^3+y^4)`
`=(2x-y)[(2x)^4+(2x)^3y+(2x)^2y^2+2xy^3+y^4)`
`=(2x)^5-y^5`
`=32x^5-y^5`
24 tháng 8 2021
a) \(40x^4-10x^2=10x^2\left(4x^2-1\right)=10x^2\left(2x-1\right)\left(2x+1\right)\)
b) \(16x^4-20x^2-y^2-5y=\left(4x^2-\dfrac{5}{2}\right)^2-\left(y-\dfrac{5}{2}\right)^2=\left(4x^2-\dfrac{5}{2}-y+\dfrac{5}{2}\right)\left(4x^2-\dfrac{5}{2}+y-\dfrac{5}{2}\right)=\left(4x^2-y\right)\left(4x^2+y-5\right)\)c)\(64a^2-9b^2-16a+1=\left(8a-1\right)^2-9b^2=\left(8a-1-3b\right)\left(8a-1+3b\right)\)d) \(5x^2+23x-10=5\left(x-\dfrac{2}{5}\right)\left(x+5\right)\)
24 tháng 8 2021
a: \(40x^4-10x^2\)
\(=10x^2\left(4x^2-1\right)\)
\(=10x^2\cdot\left(2x-1\right)\left(2x+1\right)\)
b: \(16x^4-20x^2-y^2-5y\)
\(=\left(4x^2-y\right)\left(4x^2+y\right)-5\left(4x^2+y\right)\)
\(=\left(4x^2+y\right)\left(4x^2-y-5\right)\)
c: Ta có: \(64a^2-9b^2-16a+1\)
\(=\left(8a-1\right)^2-9b^2\)
\(=\left(8a-1-3b\right)\left(8a-1+3b\right)\)
d: Ta có: \(5x^2+23x-10\)
\(=5x^2+25x-2x-10\)
\(=\left(x+5\right)\left(5x-2\right)\)
C
1
6 tháng 10 2021
\(a,=x^2y^2z^2\left(xy+yz+xz\right)\\ b,=2x\left(8x^4-1\right)\)
3 tháng 8 2021
a) Ta có: \(2x^2\left(3x^2-7x-5\right)\)
\(=2x^2\cdot3x^2-2x^2\cdot7x-2x^2\cdot5\)
\(=6x^4-14x^3-10x^2\)
c) Ta có: \(\left(16x^4-20x^2y^3-4x^5y\right):\left(-4x^2\right)\)
\(=16x^4:\left(-4x^2\right)+20x^2y^3:4x^2+4x^5y:4x^2\)
\(=-4x^3+5y^3+x^3y\)
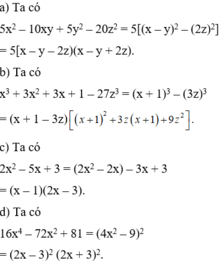
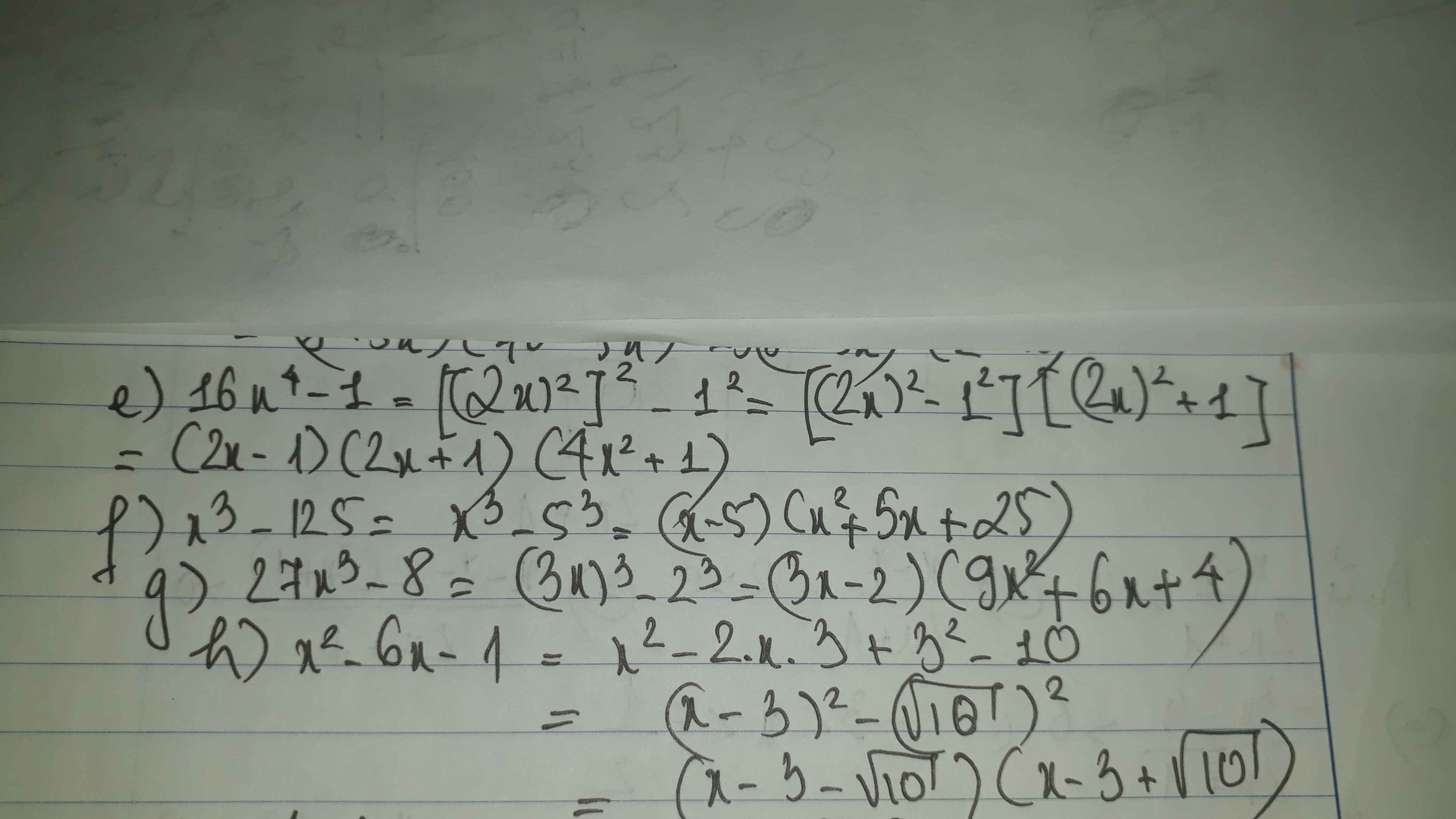
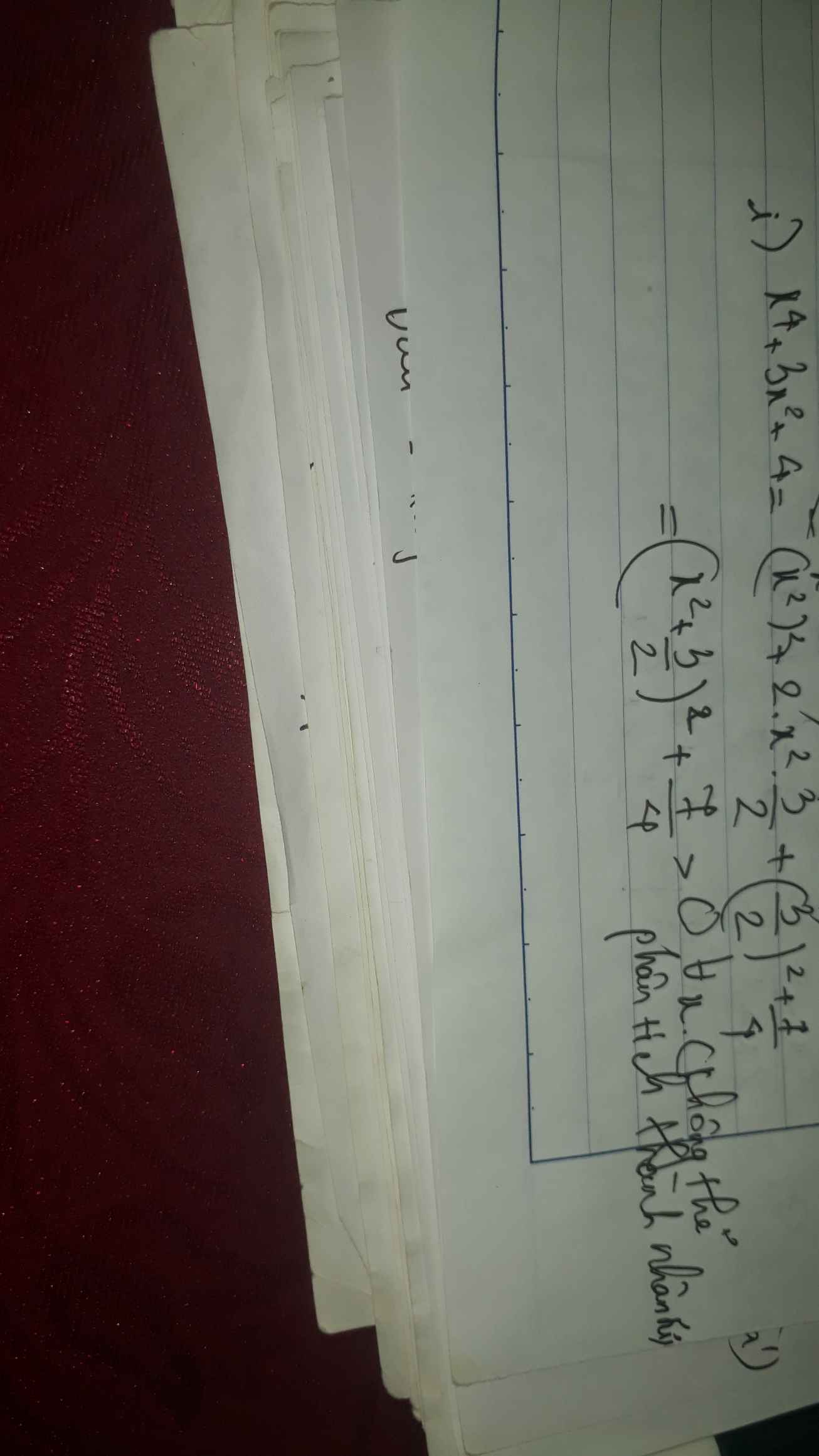
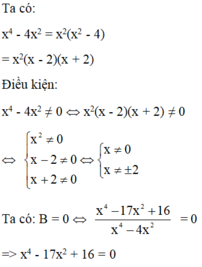
=0 nữa ạ
\(16x^4-\left(5x-1\right)^2=0\)
\(\left(4x\right)^2-\left(5x-1\right)^2=0\)
\(\left(4x-5x+1\right)\left(4x+5x-1\right)=0\)
\(\left(1-x\right)\left(9x-1\right)=0\)
⇔ 1-x =0 hoặc 9x-1 =0
=> x= 1 hoặc x= 1/9
Vậy