ND
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
18 tháng 12 2017
Lời giải:
Thể tích của chiếc hộp đó là:
\(V=x.x.h=500\Leftrightarrow x^2h=500\)
\(\Rightarrow h=\frac{500}{x^2}\)
Diện tích của chiếc hộp đó bao gồm diện tích một đáy và 4 mặt bao quanh:
\(S(x)=x^2+4xh\)
\(\Leftrightarrow S(x)=x^2+4x.\frac{500}{x^2}=x^2+\frac{2000}{x}\)
Đến đây có thể sử dụng đạo hàm rồi lập bảng biến thiên để tìm S(x) min, hoặc sử dụng cách ngắn gọn là:
Áp dụng BĐT Cô- si: \(x^2+\frac{2000}{x}=x^2+\frac{1000}{x}+\frac{1000}{x}\geq 3\sqrt[3]{x^2.\frac{1000}{x}.\frac{1000}{x}}=300\)
Hay \(S(x)\geq 300\)
Dấu bằng xảy ra khi \(x^2=\frac{1000}{x}\Leftrightarrow x=10\)
Đáp án B
CM
21 tháng 7 2018
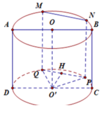
Với O'H = 4 là khoảng cách từ trục đến thiết diện và OO' = h = 8; O'P = O'Q = rd = 6
''
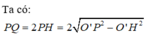
Khi đó:
CM
7 tháng 7 2018
Phương pháp:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc, khi đó 
Cách giải:
Chọn: A
12 tháng 2 2022
Bài 4 :
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=35cm\)
Bài 5 :
Theo định lí Pytago tam giác MNO vuông tại O
\(OM=\sqrt{MN^2-ON^2}=33cm\)
CM
17 tháng 5 2018
Chọn D
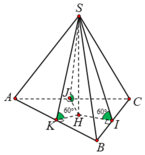
Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABC) và I, J, K là hình chiếu vuông góc của H lên các cạnh BC, CA, AB
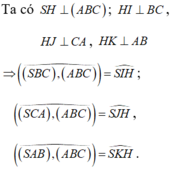
Mà các mặt bên tạo với đáy 1 góc 600 nên 
=> ΔSHJ = ΔSHI = ΔSHK (cạnh huyền – góc nhọn)
=> HI=HJ=HK => H là tâm đường tròn nội tiếp tam giác ABC
Mặt khác:
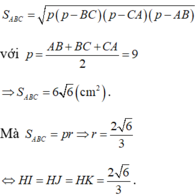
Tam giác SHI vuông tại H có SH = HI = tan 600 = 2√2
Khi đó: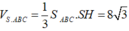 
.
PT
1
1565:5=313
4568:8=571 2135=213500