K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
1
13 tháng 2 2022
a: \(=\dfrac{9}{10}+\dfrac{1}{9}+\dfrac{7}{26}-\dfrac{1}{3}=\dfrac{554}{585}\)
b: \(=-1+\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{7}{8}+3+\dfrac{2}{9}=\dfrac{259}{72}\)
EJ
22 tháng 7 2017
a,A=1 + ( -3) + 5 + ( -7 ) + ... + 17 + ( -19 )
A=( 1 - 3 ) + ( 5 - 7 ) + ...+ ( 17 +19 )
A= (-2 ) . 10
A= (-20)
b, B= 1-4+7-10 +... -100 + 103
B= 1+ ( -4 + 7 ) + ( -10 +13 ) +...+ (-100 +103 )
B= 1 + 3 + 3 +...+3
B= 1+3 .17
B= 52
c, C= 1 + 2 -3 -4+5+6-7-8+..-99-100+101+102
C= 1 + ( 2-3-4+5) +(6-7 -8+9)+...+(98-99-100+101)+102
C= 1 + 0 + 0 + 0 + 0 + ... + 0 + 102
C= 103
3 tháng 8 2016
A = 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + ... - 99 - 100 + 101 + 102
A=(1 + 2 - 3 - 4) + (5 + 6 - 7 - 8) + ... (97 + 98 - 99 - 100) + 101 + 102
A=(-4) + (-4) +...+ (-4) + 203 ( có 25 số -4)
A=25.(-4)+203
A=-100+203
A=103
B = 1 + (-3) + 5 + (-7) + …+ 17 + (- 19)
B=[1 + (-3)] + [5 +(-7)] +...+ [17 + (-19)] Có 5 cặp số
B=(-2) + (-2) +...+ (-2) có 5 số hạng
B=(-2).5
B=-10
C = 1 - 4 + 7 - 10 + … - 100 + 103
C = (1 - 4) + (7 - 10) + … +(97- 100) + 103 có 34 cặp số
C=(-3) + (-3) +...+ (-3) +103 có 34 số -3
C=34.(-3)+103
C=-102+103
C=1
11 tháng 5 2022
a: A=(-1)+(-1)+...+(-1)+101
=101-50=51
b: B=(-3)+(-3)+...+(-3)+331
=331-330=1
NH
3
BD
5 tháng 7 2023
\(A=\dfrac{17^{100}+17^{96}+17^{92}+....+17^4+1}{17^{102}+17^{100}+17^{98}+....+17^2+1}\)
Gọi \(17^{100}+17^{96}+17^{92}+....+17^4+1\) là B
\(B=17^{100}+17^{96}+17^{92}+....+17^4+1\\ 17^4\cdot B=17^{104}+17^{100}+17^{96}+......+17^8+17^4\\ 17^4\cdot B-B=\left(17^{104}+17^{100}+17^{96}+......+17^8+17^4\right)-\left(17^{100}+17^{96}+17^{92}+....+17^4+1\right)\\ B\cdot\left(17^4-1\right)=17^{104}-1\\ B=\dfrac{17^{104}-1}{17^4-1}\)
Gọi \(17^{102}+17^{100}+17^{98}+....+17^2+1\) là C
\(C=17^{102}+17^{100}+17^{98}+....+17^2+1\\ C\cdot17^2=17^{104}+17^{102}+17^{100}+17^{98}+....+17^2\\ C\cdot17^2-C=\left(17^{104}+17^{102}+17^{100}+17^{98}+....+17^2\right)-\left(17^{102}+17^{100}+17^{98}+....+17^2+1\right)\\ C\cdot\left(17^2-1\right)=17^{104}-1\\ C=\dfrac{17^{104}-1}{17^2-1}\)
=>
\(A=B:C\\ A=\dfrac{17^{104}-1}{17^4-1}:\dfrac{17^{104}-1}{17^2-1}\\ A=\dfrac{17^2-1}{17^4-1}\)
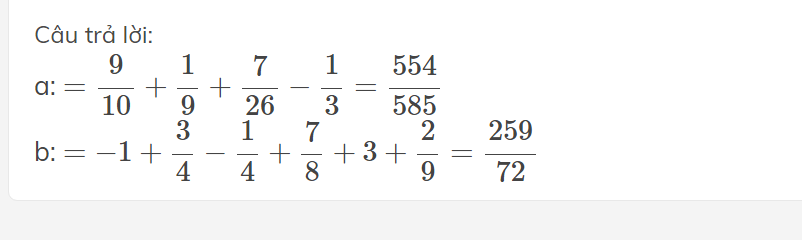
\(\left(1+4+7+...+100\right):17=a\)
\(\left\{\left(100+1\right).\left[\left(100-1\right):3+1\right].2\right\}:17=a\)
\(1717:17=a\)
\(101=a\)
Vậy...
\(\left(1+4+7+...+100\right):17=a\)
\(\Leftrightarrow\left(100+1\right).\left[\left(100-1\right):3+1\right]:2:17=a\)
\(\Leftrightarrow a=100.17:17=100.1=100.\)