K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
1
2 tháng 6 2022
Ta đặt một người ngồi cố định là người chồng
Vợ của người này có 7 vị trí có thể ngồi (trừ vị trí của chồng và hai vị trí bên trái, phải)
Lúc này trên bàn xuất hiện 2 khoảng trống để đặt ghế. Cặp vợ chồng tiếp theo chỉ có thể hoán đổi vị trí ghế ngồi với nhau ở 2 vị trí này để tránh ngồi gần. tức có 2! cách xếp
Lúc này trên bàn xuất hiện 4 khoảng trống để đặt ghế. Cặp vợ chồng tiếp theo chỉ có thể hoán đổi vị trí ghế ngồi với nhau ở 4 vị trí này để tránh ngồi gần. tức có \(A_4^2\) cách xếp
Lúc này trên bàn xuất hiện 6 khoảng trống để đặt ghế. Cặp vợ chồng tiếp theo chỉ có thể hoán đổi vị trí ghế ngồi với nhau ở 6 vị trí này để tránh ngồi gần. tức có \(A_6^2\) cách xếp
Lúc này trên bàn xuất hiện 8 khoảng trống để đặt ghế. Cặp vợ chồng tiếp theo chỉ có thể hoán đổi vị trí ghế ngồi với nhau ở 8 vị trí này để tránh ngồi gần. tức có \(A_8^2\) cách xếp
Vậy tổng số cách xếp là 7.2!\(A_4^2\).\(A_6^2\).\(A_8^2\) = 7.8!
CM
3 tháng 12 2019
Chọn C
Có 2 bộ số {a;b;c} có tổng các chữ số bằng 5 là: {0;1;4}, {0;2;3}, mỗi bộ số có 3! hoán vị nên có tất cả 12 khả năng.
Do đó xác suất để người đó bấm máy một lần đúng số cần gọi là 1 12 .
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Khả năng nhớ trung bình của nhóm học sinh đó sau 6 tháng là
\(M\left( 6 \right) = 75 - 20\ln \left( {6 + 1} \right) = 36,08179702\)%.
CM
10 tháng 8 2018
Chọn D
Gọi 2 số cuối là ab,là số điện thoại nên có đủ các chữ số từ 0 đến 9
Ta có a có 10 cách chọn, b khác a nên có 9 cách chọn. Vậy không gian mẫu có 9.10= 90 phần tử.
Vậy xá xuất gọi một lần dúng là 1/90
2 tháng 1 2023
n(A)=1
\(n\left(\Omega\right)=C^1_{10}\cdot C^1_9=90\)
=>Xác suất đúng là 1/90
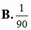
Câu 15:
$SA\perp BC$ là đúng vì $SA\perp (ABC)$
$BC\perp AB, BC\perp SA\Rightarrow BC\perp (SAB)$
$\Rightarrow BC\perp AH$ vì $AH$ thuộc $(SAB)$
$AH\perp SB; AH\perp BC\Rightarrow AH\perp (SBC)$
$\Rightarrow AH\perp SC$
Vậy đáp án A,B,C đều đúng nên D sai.
Đáp án D.
Câu 14:
$\angle (SB, (ABC))=\angle (SB, AB)=\widehat{SBA}$
$\tan \widehat{SBA}=\frac{SA}{AB}=\sqrt{3}$
$\Rightarrow \widehat{SBA}=60^0$
Đáp án D.