VT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
1
AA
4
21 tháng 8 2020
\(\left(x-\frac{3}{5}\right)=\frac{2}{5}×-\frac{1}{3}\)
\(\left(x-\frac{3}{5}\right)=-\frac{2}{165}\)
\(x=-\frac{2}{165}+\frac{3}{5}\)
\(x=\frac{97}{165}\)
vậy \(x=\frac{97}{165}\)
\(x×\left(\frac{3}{7}+\frac{2}{3}\right)=\frac{10}{21}\)
\(x×\frac{23}{21}=\frac{10}{21}\)
\(x=\frac{10}{21}:\frac{23}{21}\)
\(x=\frac{10}{23}\)
vậy \(x=\frac{10}{23}\)
21 tháng 8 2020
\(\left(x-\frac{3}{5}\right):\frac{-1}{3}=\frac{2}{5}\)
=> \(x-\frac{3}{5}=\frac{2}{5}\cdot\left(-\frac{1}{3}\right)=-\frac{2}{15}\)
=> \(x=-\frac{2}{15}+\frac{3}{5}=-\frac{2}{15}+\frac{9}{15}=\frac{7}{15}\)
\(\frac{3}{7}x-\frac{2}{3}x=\frac{10}{21}\)
=> \(\left(\frac{3}{7}-\frac{2}{3}\right)x=\frac{10}{21}\)
=> \(-\frac{5}{21}x=\frac{10}{21}\)
=> \(x=\frac{10}{21}:\frac{-5}{21}=\frac{10}{21}\cdot\frac{-21}{5}=-2\)
Hai bài của ☆luffy cute☆ đều sai hết , xem xét lại đi nhé
15 tháng 9 2021
a) \(\dfrac{1}{4}-3\left(\dfrac{1}{12}+\dfrac{3}{8}\right)=\dfrac{1}{4}-\dfrac{1}{4}-\dfrac{9}{8}=-\dfrac{9}{8}\)
b) \(\left(-\dfrac{2}{3}+\dfrac{3}{5}\right):\dfrac{1}{50}-30=\left(-\dfrac{2}{3}+\dfrac{3}{5}\right).50-30=-\dfrac{100}{3}+30-30=-\dfrac{100}{3}\)
giúp mk với, mk cần gấp, mn nêu cả lời giải chi tiêt 1 chút giúp mk nhé, cam on mn rất nhìu ạ
1 tháng 11 2021
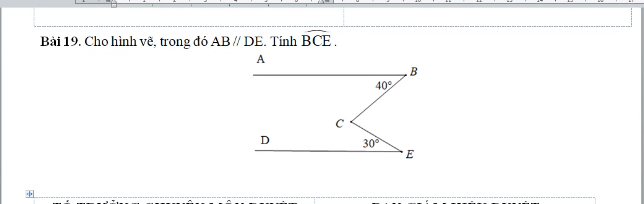
Kẻ CF//AB thì CF//DE
Do đó \(\widehat{BCF}=\widehat{ABC}=40^0;\widehat{FCE}=\widehat{CED}=30^0\) (so le trong)
Vậy \(\widehat{BCE}=\widehat{BCF}+\widehat{FCE}=30^0+40^0=70^0\)
NQ
0
23 tháng 7 2023
A) \(...=\left(7y-3\right)^3\)
B) \(...=\left(4y-3\right)^3\)
C) \(...=x^4+2x^2+1-\left(y^2+2y+1\right)\)
\(=\left(x^2+1\right)^2-\left(y+1\right)^2\)
D) \(...=x^2-6x+9-\left(y^2-10y+25\right)\)
\(=\left(x-3\right)^2-\left(y-5\right)^2\)
KK
1
2 tháng 3 2020
\(2^x:1+2^x:2+...+2^x:49=2^{49}-1\)
\(2^x.1+2^x.\frac{1}{2}+...+2^x.\frac{1}{49}=2^{49}-1\)
\(2^x.\left(1+\frac{1}{2}+...+\frac{1}{49}\right)=2^{49}-1\)
3 tháng 3 2020
Đặt: \(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\)
=> \(2A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\)
=> \(2A-A=\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^{49}}\right)\)
=> \(A=1-\frac{1}{2^{49}}=\frac{2^{49}-1}{2^{49}}\)
\(2^{x-1}+2^{x-2}+2^{x-3}+...+2^{x-49}=2^{49}-1\)
<=> \(\frac{2^x}{2}+\frac{2^x}{2^2}+\frac{2^x}{2^3}+...+\frac{2^x}{2^{49}}=2^{49}-1\)
<=> \(2^x\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\right)=2^{49}-1\)
<=> \(2^x.\frac{2^{49}-1}{2^{49}}=2^{49}-1\)
<=> \(2^x=2^{49}\)
<=> x = 49.
- \(\dfrac{1}{12}\) - ( 2 \(\dfrac{5}{8}\) - \(\dfrac{1}{3}\))
= - \(\dfrac{1}{12}\) - ( \(\dfrac{21}{8}\) - \(\dfrac{1}{3}\))
= - \(\dfrac{1}{12}\) - ( \(\dfrac{63}{24}\) - \(\dfrac{8}{24}\))
= - \(\dfrac{1}{12}\) - \(\dfrac{55}{24}\)
= - \(\dfrac{2}{24}\) - \(\dfrac{55}{24}\)
= - \(\dfrac{57}{24}\)
= - \(\dfrac{19}{8}\)
`(-1)/12 - (2 5/8 - 1/3)`
`=(-1)/12 - ( 21/8 - 1/2)`
`=(-1)/12 - (63/24 - 8/12)`
`=(-1)/12 -55/24`
`=(-2)/24 - 55/24`
`=(-2-55)/24`
`=(-57)/24`
`=(-19)/8`