Câu 7: Tìm số phức liên hợp của số phức z=1−2iz=1−2i
A. 2−i2−i
B. −1−2i−1−2i
C. −1+2i−1+2i
D. 1+2i1+2i
Câu 8: Trong không gian Oxyz, cho hai điểm A(−1;2;3)A(−1;2;3) và B(3;0;−2)B(3;0;−2). Tìm tọa độ của vectơ −−→AB.AB→.
A. −−→AB=(−4;2;5)AB→=(−4;2;5)
B. −−→AB=(1;1;12)AB→=(1;1;12)
C. −−→AB=(2;2;1)AB→=(2;2;1)
D. −−→AB=(4;−2;−5)AB→=(4;−2;−5)
Câu 9: Trong không gian Oxyz, mặt phẳng (P)(P) đi qua điểm A(1;2;0)A(1;2;0) và vuông góc với đường thẳng d:x+12=y1=z−1−1d:x+12=y1=z−1−1 có phương trình là
A. x+2y−z+4=0x+2y−z+4=0
B. 2x−y−z+4=02x−y−z+4=0
C. 2x+y−z−4=02x+y−z−4=0
D. 2x+y+z−4=02x+y+z−4=0
Câu 10: Họ nguyên hàm của hàm số f(x)=4x3f(x)=4x3 là
A. 4x4+C4x4+C
B. 12x2+C12x2+C
C. x44+Cx44+C
D. x4+Cx4+C
Câu 11: Công thức nguyên hàm nào sau đây đúng?
A. ∫exdx=−ex+C∫exdx=−ex+C
B. ∫dx=x+C∫dx=x+C
C. ∫1xdx=−lnx+C∫1xdx=−lnx+C
D. ∫cosxdx=−sinx+C∫cosxdx=−sinx+C
Câu 12: Trong không gian Oxyz, cho →a=(−1;3;2)a→=(−1;3;2) và →b=(−3;−1;2)b→=(−3;−1;2). Tính →a.→b.a→.b→.
A. 2
B. 10
C. 3
D. 4
Câu 13: Trong không gian Oxyz, điểm M(3;4;−2)M(3;4;−2) thuộc mặt phẳng nào trong các mặt phẳng sau?
A. (S):x+y+z+5=0(S):x+y+z+5=0
B. (Q):x−1=0(Q):x−1=0
C. (R):x+y−7=0(R):x+y−7=0
D. (P):z−2=0(P):z−2=0
Câu 14: Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt cầu tâm I(1;0;−3)I(1;0;−3)và bán kính R=3R=3?
A. (x−1)2+y2+(z+3)2=9(x−1)2+y2+(z+3)2=9
B. (x−1)2+y2+(z+3)2=3(x−1)2+y2+(z+3)2=3
C. (x+1)2+y2+(z−3)2=3(x+1)2+y2+(z−3)2=3
D. (x+1)2+y2+(z−3)2=9(x+1)2+y2+(z−3)2=9
Câu 15: Trong không gian Oxyz, phương trình mặt phẳng (P)(P) đi qua điểm M(−1;2;0)M(−1;2;0) và có vectơ pháp tuyến →n=(4;0;−5)n→=(4;0;−5) là
A. 4x−5y−4=04x−5y−4=0
B. 4x−5z−4=04x−5z−4=0
C. 4x−5y+4=04x−5y+4=0
D. 4x−5z+4=04x−5z+4=0
Câu 16: Nghiệm của phương trình (3+i)z+(4−5i)=6−3i(3+i)z+(4−5i)=6−3i là
A. z=25+45iz=25+45i
B. z=12+12iz=12+12i
C. z=45+25iz=45+25i
D. z=1+12iz=1+12i
Câu 17: Trong không gian Oxyz, mặt phẳng đi qua tâm của mặt cầu (x−1)2+(y+2)2+z2=12(x−1)2+(y+2)2+z2=12 và song song với mặt phẳng (Oxz)(Oxz)có phương trình là
A. y+2=0y+2=0
B. x+z−1=0x+z−1=0
C. y−2=0y−2=0
D. y+1=0y+1=0
Câu 18: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x2−2xy=x2−2x và trục hoành.
A. 2
B. 4343
C. 203203
D. −43−43
Câu 19: Cho F(x)F(x) là một nguyên hàm củaf(x)f(x) trên RR và F(0)=2,F(0)=2, F(3)=7F(3)=7. Tính 3∫0f(x)dx.∫03f(x)dx.
A. 9
B. -9
C. 5
D. -5
Câu 20: Gọi z1,z2z1,z2 là hai nghiệm phức của phương trình z2−6z+14=0z2−6z+14=0. Tính S=|z1|+|z2|.S=|z1|+|z2|.
A. S=3√2S=32
B. S=2√6S=26
C. S=4√3S=43
D. S=2√14S=214
Câu 21: Trong không gian Oxyz, tính khoảng cách giữa hai mặt phẳng (P):2x+2y−z−11=0(P):2x+2y−z−11=0 và (Q):2x+2y−z+4=0(Q):2x+2y−z+4=0.
A. d((P),(Q))=5d((P),(Q))=5
B. d((P),(Q))=3d((P),(Q))=3
C. d((P),(Q))=1d((P),(Q))=1
D. d((P),(Q))=4d((P),(Q))=4
Câu 22: Cho z=1+√3iz=1+3i. Tìm số phức nghịch đảo của số phức zz.
A. 1z=14+√34i1z=14+34i
B. 1z=12−√32i1z=12−32i
C. 1z=12+√32i1z=12+32i
D. 1z=14−√34i1z=14−34i
Câu 23: Tính tích phân I=2019∫0e2xdx.I=∫02019e2xdx.
A. I=12e4038I=12e4038
B. I=12e4038−1I=12e4038−1
C. I=12(e4038−1)I=12(e4038−1)
D. e4038−1

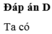
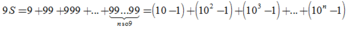
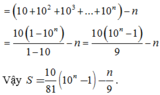




111+111=222 nha!
lộn nha bằng 222