K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
5 tháng 9 2020
Lời giải:
Ta thấy:
$10x\equiv 0\pmod 5$
$288\equiv 3\pmod 5$
$\Rightarrow y^2\equiv 3\pmod 5$ (vô lý)
Do ta biết rằng một số chính phương khi chia cho $5$ chỉ có thể có dư là $0,1,4$.
Như vậy, không tồn tại số tự nhiên $x,y$ thỏa mãn điều kiện đề bài.
MS
1
5 tháng 12 2017
Ta có: \(10x+23=5\left(2x+1\right)+18\)
Để\(10x+23⋮\left(2x+1\right)\)thì \(18⋮\left(2x+1\right)\Rightarrow2x+1\inƯ\left(18\right)\)Mà \(2x+1\in N\)và 2x+1 là số lẻ
\(\Rightarrow2x+1\in\left(1;3;9\right)\)
\(\Rightarrow x\in\left(0;1;4\right)\)
Vậy...............................................
DN
1
HT
20 tháng 7 2015
7x + 8x + 9x + 10x +.....+ 201x - 280 = 20000
=> (7+8+9+10+....+201)x = 20280
=> 20280x = 20280
=> x = 20280 : 20280
=> x = 1
DN
0
6 tháng 4 2017
Ta có 10x+23:2x+1
2x+1:2x+1 ( tớ viết dấu : thay cho chia hết nhé)
=>10x+23 : 2x+1
5.(2x+1):2x+1
=>10x+23:2x+1
10x+5:2x+1
=>(10x+23)-(10x+5):2x+1
=>18:2x+1
Vì x thuộc N nên 2x+1 thuộc N
=> 2x+1\(\in\){1;3;9}, vì 2x+1 lẻ
=>x \(\in\){0;1;4}
TS
4
XO
11 tháng 7 2019
Ta có : \(10x+23⋮2x+1\)
\(\Rightarrow10x+5+18⋮2x+1\)
\(\Rightarrow5\left(2x+1\right)+18⋮2x+1\)
Ta có Vì \(5\left(2x+1\right)⋮2x+1\)
\(\Rightarrow18⋮2x+1\)
\(\Rightarrow2x+1\inƯ\left(18\right)\)
Với \(x\inℕ\Rightarrow2x+1\inℕ\)
\(\Rightarrow2x+1\in\left\{1;2;3;6;9;18\right\}\)
Lập bảng xét các trường hợp:
| \(2x+1\) | \(1\) | \(2\) | \(3\) | \(6\) | \(9\) | \(18\) |
| \(x\) | \(0\) | \(\frac{1}{2}\) | \(1\) | \(\frac{5}{2}\) | \(4\) | \(\frac{17}{2}\) |
Vậy \(x\inℕ\)thỏa mãn là 0 ; 1 ; 4
T
11 tháng 7 2019
#)Giải :
Ta có :
\(10x+32=10x+5+18=5\left(2x+1\right)+18\) chia hết cho 2x + 1
\(\Rightarrow\) 18 chia hết cho 2x + 1
\(\Rightarrow2x+1\inƯ\left(18\right)=\left\{1;2;3;6;9;18\right\}\)
Mà 2x + 1 lại là số lẻ
\(\Rightarrow2x+1\in\left\{1;3;9\right\}\)
\(\Rightarrow x\in\left\{0;1;4\right\}\)
PT
1
NQ
1
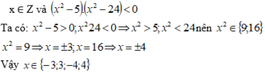
Ta có:
\(10x+x^2=56\)
\(\Rightarrow x\left(10+x\right)=56\)
Ta có: \(56=1.56=2.28=4.14=7.8\)
Mà \(x\left(10+x\right)\)là tích của 2 số tự nhiên hơn kém nhau 10 đơn vị
\(\Rightarrow x=4\)
x =4 nha bạn