Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=\dfrac{-3}{\left(x-1\right)^2}\)
Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\dfrac{-3}{\left(x_0-1\right)^2}\left(x-x_0\right)+\dfrac{2x_0+1}{x_0-1}\) (1)
a.
Tọa độ A và B có dạng: \(A\left(\dfrac{2x_0^2+2x_0-1}{3};0\right)\) ; \(B\left(0;\dfrac{2x_0^2+2x_0-1}{\left(x_0-1\right)^2}\right)\)
\(\Rightarrow OA=\left|\dfrac{2x_0^2+2x_0-1}{3}\right|;OB=\dfrac{\left|2x_0^2+2x_0-1\right|}{\left(x_0-1\right)^2}\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{6}\Rightarrow OA.OB=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{\left(2x_0^2+2x_0-1\right)^2}{3\left(x_0-1\right)^2}=\dfrac{1}{3}\Rightarrow\left(2x_0^2+2x_0-1\right)^2=\left(x_0-1\right)^2\)
\(\Leftrightarrow\left(2x_0^2+3x_0-2\right)\left(2x_0^2+x_0\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=0\\x_0=-\dfrac{1}{2}\\x_0=-2\\x_0=\dfrac{1}{2}\end{matrix}\right.\)
Có 4 tiếp tuyến thỏa mãn:... (thế lần lượt các giá trị \(x_0\) vào (1) là được)

gọi số cần tìm là abcdef
a có 4 cách chọn
+ với a = { 1,2,3}
b có 5 cách chọn
c có 4 cách chọn
d có 3 cách chọn
e có 2 cách chọn
f có 1 cách chọn
\(\Rightarrow\) có 360 số
+ với a = 4
b có 3 cách chọn
b={ 1,2}
c có 4 cách chọn
d có́ 3 cách chọn
e có 2 cách choṇ
f có 1 cách chọn
b =3
c có 1 cách chọn
d có 3 cách chọn
e có 2 cách chọn
f có 1 cách chọn
\(\Rightarrow\)có 54 số
vậy có 360 + 54 = 414 số

a)
Gọi abcde là 5 chữ số khác nhau cần tìm
a-9cc
b \ {a} - 8cc
...
e \ {a,b,c,d} - 5cc
<=> 9*8*7*6*5=9P5=15120 số
b)
e {2,4,6,8} - 4cc
a \ {e} - 8cc
b \ {a,e} - 7cc
c \ {a,b,e} - 6cc
d \ {a,b,c,e} - 5cc
<=> 4 * 8P4 = 6720 số
a.
Có \(A_9^5=15120\) cách
b.
Gọi số đó là \(\overline{abcde}\) \(\Rightarrow e\) chẵn \(\Rightarrow e\) có 4 cách chọn
Bộ abcd có \(A_8^4=1680\) cách
tổng cộng: \(4.1680=...\) cách

\(1+2+3+4+5+6=21\) chia hết cho 3
\(\Rightarrow\) Để tạo ra số có 4 chữ số chia hết cho 3 ta cần loại ra 2 chữ số có tổng chia hết cho 3
\(\Rightarrow\) 2 số đó cùng chia hết cho 3 hoặc (1 số chia 3 dư 1, 1 số chia 3 dư 2)
\(\Rightarrow\) Các cặp (3;6);(1;2);(1;5);(2;4) có 4 cặp
\(\Rightarrow\) Có 4 bộ 4 chữ số tương ứng có tổng chia hết cho 3
\(\Rightarrow4.4!=96\) số thỏa mãn

Chọn C
Giả sử số lập được có dạng ![]()
![]()
Ta có 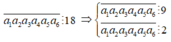
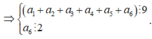
Vì ![]() nên ta có các trường hợp sau
nên ta có các trường hợp sau
Trường hợp 1:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ ![]()
+ Có 3 cách chọn chọn a 6
+ Có 5! cách chọn chọn bộ 5 số ![]()
Suy ra có 3.5! = 360 số.
Trường hợp 2:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ ![]()
+
a
6
= 0, có 5! cách chọn bộ 5 số ![]()
+
a
6
≠
0 khi đó
a
6
có 3 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ ![]()
+
a
6
= 0, có 5! cách chọn bộ 5 số ![]()
+
a
6
≠
0 khi đó
a
6
có 1 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.
1. Ta chia các số thành 3 tập \(A=\left\{3;6\right\};B=\left\{1;4\right\};C=\left\{2;5\right\}\) có số dư khi chia 3 lần lượt là 0,1,2
Số chia hết cho 3 khi tổng các chữ số chia hết cho 3 \(\Rightarrow\) các chữ số phải được tạo thành bằng cách lấy 1 số từ tập A, 1 chữ số từ tập B, 1 chữ số thuộc tập C
\(\Rightarrow2.2.2=8\) cách chọn
Hoán vị 3 chữ số: \(3!=6\) cách
\(\Rightarrow8.6=48\) số thỏa mãn
2. Câu này đề là cắt Ox, Oy hay cắt "trục Ox, Oy" hay cắt "tia Ox, Oy" nhỉ?
Nếu là trục thì có vài trường hợp cần xét, tia thì chỉ cần xét 1 trường hợp thôi
2.
Do đường thẳng cắt tia Ox, Oy tại A và B, gọi \(A\left(a;0\right)\) và \(B\left(0;b\right)\) với \(\left\{{}\begin{matrix}0< a< 3\\0< b< 2\end{matrix}\right.\)
Phương trình đường thẳng dạng đoạn chắn: \(\dfrac{x}{a}+\dfrac{y}{b}=1\)
Do đường thẳng qua M nên:
\(\dfrac{3}{a}+\dfrac{2}{b}=1\Leftrightarrow b=\dfrac{2a}{a-3}\)
\(\Rightarrow S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}ab=\dfrac{a^2}{a-3}=\dfrac{\left(a-3\right)\left(a+3\right)+9}{a-3}\)
\(S=a+3+\dfrac{9}{a-3}=a-3+\dfrac{9}{a-3}+6\ge2\sqrt{\dfrac{9\left(a-3\right)}{a-3}}+6=12\)
Dấu = xảy ra khi \(a-3=\dfrac{9}{a-3}\Rightarrow a=6\Rightarrow b=4\)
\(\Rightarrow\dfrac{x}{6}+\dfrac{y}{4}=1\Leftrightarrow2x+3y-12=0\)