Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)
\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)\(\)(đpcm)
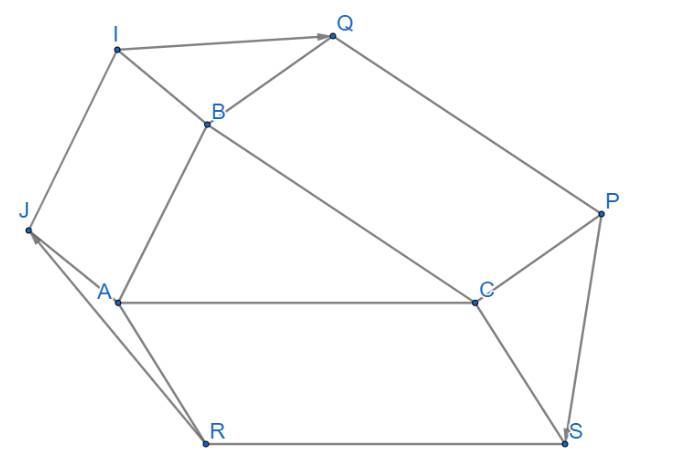

Có \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{RA}+\overrightarrow{AJ}+\overrightarrow{IB}+\overrightarrow{BQ}+\overrightarrow{PC}+\overrightarrow{CS}\)
\(=\left(\overrightarrow{RA}+\overrightarrow{CS}\right)+\left(\overrightarrow{AJ}+\overrightarrow{IB}\right)+\left(\overrightarrow{BQ}+\overrightarrow{PC}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\). ( Do tứ giác ABIJ, BCPQ, CARS là hình bình hành).
Vậy \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{0}\).

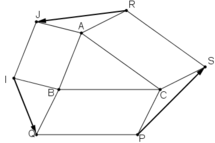
Ta có:
AJIB là hình bình hành nên 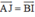
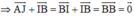
Tương tự như vậy:
BCPQ là hình bình hành nên 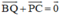
CARS là hình bình hành nên 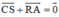
Do đó:


1. MA + MC = MB +MD
<=> MA + MC = MA + AB + MC + CD
<=>MA + MC = MA + MC +0
2.
RJ+IQ+PS=RA+ẠJ+IB+BQ+PC+CS
= (RA+CS) + (AJ+IB) + (BQ+PC)
= 0+0+0=0

Ta đã biết nếu G' là trọng tâm tam giác ABC thì:
\(\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\).
Gỉa sử có điểm G thỏa mãn: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Ta sẽ chứng minh \(G\equiv G'\).
Thật vậy:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}+\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GG'}=\overrightarrow{0}\).
Vậy \(G\equiv G'\).
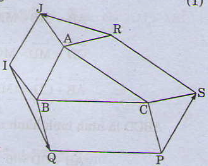
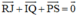
Bài 1 : Ta có :
\(VT=\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{RA}+\overrightarrow{AJ}+\overrightarrow{IB}+\overrightarrow{BQ}+\overrightarrow{PC}+\overrightarrow{CS}\)
Mà : \(\left\{{}\begin{matrix}\overrightarrow{RA}=\overrightarrow{SC}\\\overrightarrow{AJ}=\overrightarrow{BI}\\\overrightarrow{BQ}=\overrightarrow{CP}\end{matrix}\right.\) ( Tính chất hình bình hành )
\(\Rightarrow VT=\overrightarrow{SC}+\overrightarrow{CS}+\overrightarrow{BI}+\overrightarrow{IB}+\overrightarrow{CP}+\overrightarrow{PC}\)
\(=\overrightarrow{SC}-\overrightarrow{SC}+\overrightarrow{BI}-\overrightarrow{BI}+\overrightarrow{CP}-\overrightarrow{CP}=0\) ( đpcm )
Câu 2 : Gọi \(AM\) là đường trung tuyến của \(\Delta ABC\) và lấy D đối xứng với G qua M .
Theo quy tắc hình bình hành ta có :
\(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\left(1\right)\)
Mà : \(\overrightarrow{GA}=\overrightarrow{DG}\Rightarrow\overrightarrow{GA}+\overrightarrow{GD}=0\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GA}+\overrightarrow{GD}=0\) (đpcm)
2)
Gọi I là giao điểm của AG và BC
=> I là trung điểm BC
Tên tia đối tia IG lấy H sao cho I là trung điểm GH
=> Tứ giác BGCH là hình bình hành
\(\text{Ta có : }AG=\frac{2}{3}AI=2\cdot\frac{1}{3}AI=2GI\left(\text{Tính chát trọng tâm }\Delta\right)\\ GH=2GI\left(I\text{ là trung điểm }GH\right)\\ \Rightarrow AG=GH\\ \Rightarrow\overrightarrow{GA}+\overrightarrow{GH}=0\\ \text{Mà theo quy tắc hình bình hành }:\overrightarrow{GB}+\overrightarrow{GC}=GH\\ \Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GA}+\overrightarrow{GH}=0\)