Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
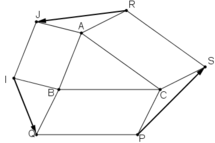
Có \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{RA}+\overrightarrow{AJ}+\overrightarrow{IB}+\overrightarrow{BQ}+\overrightarrow{PC}+\overrightarrow{CS}\)
\(=\left(\overrightarrow{RA}+\overrightarrow{CS}\right)+\left(\overrightarrow{AJ}+\overrightarrow{IB}\right)+\left(\overrightarrow{BQ}+\overrightarrow{PC}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\). ( Do tứ giác ABIJ, BCPQ, CARS là hình bình hành).
Vậy \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{0}\).
\(\overrightarrow{RF}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{RA}+\overrightarrow{AF}+\overrightarrow{IB}+\overrightarrow{BQ}+\overrightarrow{PC}+\overrightarrow{CS}=\overrightarrow{0}\)
ta có : \(\overrightarrow{RF}+\overrightarrow{IQ}+\overrightarrow{PS}\)
\(=\overrightarrow{RA}+\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{IB}+\overrightarrow{BC}+\overrightarrow{CQ}+\overrightarrow{PC}+\overrightarrow{CA}+\overrightarrow{AS}\)
\(=\overrightarrow{RA}+\overrightarrow{BF}+\overrightarrow{IB}+\overrightarrow{CQ}+\overrightarrow{PC}+\overrightarrow{AS}\) \(=\overrightarrow{RS}+\overrightarrow{IF}+\overrightarrow{PQ}=\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{0}\left(đpcm\right)\)
Ta có:
AJIB là hình bình hành nên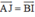 
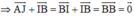
Tương tự như vậy:
BCPQ là hình bình hành nên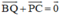 
CARS là hình bình hành nên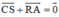 
Do đó:
bài 1) ta có \(\overrightarrow{AQ}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NP}+\overrightarrow{PQ}=\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{BC}\)
\(=\left(\overrightarrow{BA}+\overrightarrow{BC}\right)+\left(\overrightarrow{DA}+\overrightarrow{DC}\right)=\overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}\left(đpcm\right)\)
bài 2) bn tham khảo nha : https://hoc24.vn/hoi-dap/question/636668.html
Ta đã biết nếu G' là trọng tâm tam giác ABC thì:
\(\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\).
Gỉa sử có điểm G thỏa mãn: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Ta sẽ chứng minh \(G\equiv G'\).
Thật vậy:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}+\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GG'}=\overrightarrow{0}\).
Vậy \(G\equiv G'\).
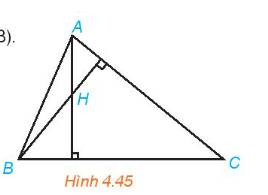
a) \( AH \bot BC\) và \(BH \bot CA\)
\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) . Do đó \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \)
Tương tự suy ra \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \).
b) Gọi H có tọa độ (x; y)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} = (x - ( - 1);y - 2) = (x + 1;y - 2)\\\overrightarrow {BH} = (x - 8;y - ( - 1)) = (x - 8;y + 1)\end{array} \right.\)
Ta có: \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BC} = (8 - 8;8 - ( - 1)) = (0;9)\)
\((x + 1).0 + (y - 2).9 = 0 \Leftrightarrow 9.(y - 2) = 0 \Leftrightarrow y = 2.\)
Lại có: \(\overrightarrow {BH} .\overrightarrow {CA} = \overrightarrow 0 \) và \(\overrightarrow {CA} = ( - 1 - 8;2 - 8) = ( - 9; - 6)\)
\(\begin{array}{l}(x - 8).( - 9) + (y + 1).( - 6) = 0\\ \Leftrightarrow - 9x + 72 + 3.( - 6) = 0\\ \Leftrightarrow - 9x + 54 = 0\\ \Leftrightarrow x = 6.\end{array}\)
Vậy H có tọa độ (6; 2)
c) Ta có: \(\overrightarrow {AB} = (8 - ( - 1); - 1 - 2) = (9; - 3)\)\( \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{9^2} + {{( - 3)}^2}} = 3\sqrt {10} \)
Và \(\overrightarrow {BC} = (0;9) \Rightarrow BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {9^2}} = 9\);
\(\overrightarrow {CA} = ( - 9; - 6)\)\( \Rightarrow AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{{( - 9)}^2} + {{( - 6)}^2}} = 3\sqrt {13} .\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt {13} } \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( 9 \right)}^2}}}{{2.3\sqrt {13} .3\sqrt {10} }} \approx 0,614\)\( \Rightarrow \widehat A \approx 52,{125^o}\)
\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 9 \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( {3\sqrt {13} } \right)}^2}}}{{2.9.3\sqrt {10} }} = \frac{{\sqrt {10} }}{{10}}\)\( \Rightarrow \widehat B \approx 71,{565^o}\)
\( \Rightarrow \widehat C \approx 56,{31^o}\)
Vậy tam giác ABC có: \(a = 9;b = 3\sqrt {13} ;c = 3\sqrt {10} \); \(\widehat A \approx 52,{125^o};\widehat B \approx 71,{565^o};\widehat C \approx 56,{31^o}.\)
Cách 1:
Gọi O là giao điểm của AC và BD.
Ta có:
\(\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {DA} + \overrightarrow {BG} = - \overrightarrow b + \overrightarrow {BG} ;\end{array}\)(*)
Lại có: \(\overrightarrow {BD} =\overrightarrow {BA} + \overrightarrow {AD} = - \overrightarrow a + \overrightarrow b \).
\(\overrightarrow {BG} ,\overrightarrow {BD} \) cùng phương và \(\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|\)
\( \Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)\)
Do đó (*) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = -\overrightarrow b + \overrightarrow {BG} = -\overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b ;\end{array} \right.\)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)
Cách 2:
Gọi AE, CF là các trung tuyến trong tam giác ABC.
Ta có:
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)} \right] \\= \frac{1}{3}\left( {2\overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {CG} = \frac{2}{3}\overrightarrow {CF} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right] = \frac{1}{3}\left( {2\overrightarrow {CB} + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD} - \overrightarrow {AB} } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b \)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)
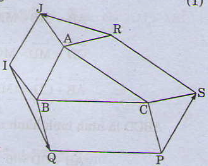
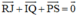
\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)
\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)\(\)(đpcm)