Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Góc C + góc KBC = 90 độ, góc C + HAC=90 độ nên góc HBP= góc NAH
HBP+HPB=90 độ, HPB=APQ (đối đỉnh) nên NAH+APQ=90 độ nên AN vuông góc với BQ
b, Tam giác APQ có đường cao cũng là đường phân giác nên tamg giác PAQ cân do đó AN cũng là đường trung trục của tam giác APQ, nên MP=MQ, tương tự sẽ có NP=MP=NP=MQ
do đó MPNQ là hình vuông

a: BC=căn 9^2+12^2=15cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=15/7
=>BD=45/7cm; CD=60/7cm
AH=9*12/15=108/15=7,2cm
b: Xét ΔHAC vuông tại H và ΔMEA vuông tại M có
góc HCA=góc MAE
=>ΔHAC đồng dạng với ΔMEA

1: Xét ΔAEI vuông tại I và ΔBEH vuông tại H có
góc AEI=góc BEH
=>ΔAEI đồng dạng với ΔBEH
2: Xét ΔBAF và ΔBKF co
BA=BK
góc ABF=góc KBF
BF chung
=>ΔBAF=ΔBKF
=>góc BKF=90 độ
=>FK vuông góc BC
=>FK//AE
Xét ΔBAK có
AH,BI là đường cao
AH cắt BI tại E
=>E là trực tâm
=>KE vuông góc AB
=>KE//AF
ΔBAK cân tại B
mà BI là đường cao
nên BI là trung trực của AK
=>EA=EK
Xét tứ giác AEKF có
KE//AF
FK//AE
EK=EA
=>AEKF là hình thoi

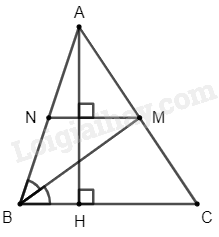
a) Ta có:
\(NM \bot AH\) (gt)
\(BC \bot AH\) (gt)
Suy ra \(NM\) // \(BC\)
Suy ra \(BNMC\) là hình thang
b) Vì \(NM\) // \(BC\) (cmt)
Suy ra \(\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}\) (so le trong)
Mà \(\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}\) (do \(MB\) là phân giác)
Suy ra \(\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}\)
Suy ra \(\Delta MNB\) cân tại \(N\)
Suy ra \(BN = NM\)
