Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) S, I, J, G là điểm chunng của (SAE) và (SBD)
b) S, K, L là điểm chung của (SAB) và (SDE)

Bài 3:
Bạn coi lại đề, ko có mặt phẳng nào là mặt phẳng S.ABCD cả :)
Bài 4:
Qua S kẻ đường thẳng d song song AD và BC
Ba mặt phẳng (SAD); (SBC); (ABCD) cắt nhau theo hai giao tuyến AD và BC song song nhau nên giao tuyến thứ 3 cũng phải song song AD và BC
\(\Rightarrow\) Đường thẳng d vừa dựng là giao tuyến cần tìm
Bài 5:
Trong mặt phẳng (SAD), qua M kẻ đường thẳng song song SD cắt AD tại N
Trong mặt phẳng (ABCD), qua N kẻ đường thẳng song song AC cắt CD tại P
Trong mặt phẳng (SAC), qua M kẻ đường thẳng song song AC cắt SC tại Q
Trong mặt phẳng (ABCD), nối NP kéo dài cắt BC tại K
Trong mặt phẳng (SBC), nối K và Q kéo dài cắt SB tại H
Ngũ giác MNPQH là thiết diện cần tìm

Bài 2:
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SAD\right)\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\) AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(tan\widehat{SCA}=\frac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
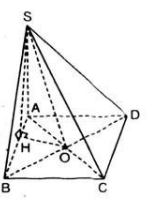
Bài 1:
Do O là tâm đáy \(\Rightarrow\) O là trung điểm AC và BD
\(SA=SC\Rightarrow\Delta SAC\) cân tại S \(\Rightarrow SO\perp AC\) (trung tuyến đồng thời là đường cao) (1)
Tương tự \(\Delta SBD\) cân tại S \(\Rightarrow SO\perp BD\) (2)
(1);(2) \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow DO\) là hình chiếu của SD lên (ABCD) \(\Rightarrow\widehat{SDO}\) là góc giữa SD và (ABCD)
\(SD=SB=2a\Rightarrow sin\widehat{SDO}=\frac{SO}{SD}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{SDO}=60^0\)

S A B C D O M I J
a/\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\Rightarrow\Delta SAB\) vuông tại A
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\Rightarrow\Delta SAD\) vuông tại A
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\)
Mà \(CD\perp AD\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\Rightarrow\Delta SCD\) vuông tại D
Tương tự \(\left\{{}\begin{matrix}BC\perp AB\\BC\perp SA\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\Rightarrow\Delta SBC\) vuông tại B
b/ \(\left\{{}\begin{matrix}BD\in\left(ABCD\right)\\SA\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow BD\perp SA\)
Lại có \(BD\perp AC\) (t/c hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\)
\(\left\{{}\begin{matrix}AB\perp SA\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp SD\)
c/ Ta có O là trung điểm AC; M là trung điểm SC \(\Rightarrow MO\) là đường trung bình trong \(\Delta SAC\)
\(\Rightarrow MO//SA\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow MO\perp\left(ABCD\right)\)
Trong tam giác vuông \(SBC\) có \(BM\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow BM=\dfrac{1}{2}SC=MS=MC\)
Tương tự, trong tam giác vuông \(SCD\) có \(DM\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow DM=\dfrac{1}{2}SC=MS=MC\)
Lại có \(SA\perp AC\) (do \(SA\perp\left(ABCD\right)\)) \(\Rightarrow\Delta SAC\) vuông tại A
\(\Rightarrow\) trong tam giác vuông SAC có AM là trung tuyến
\(\Rightarrow AM=\dfrac{1}{2}SC\)
\(\Rightarrow MA=MB=MC=MD=MS\)
d/
Do I là trung điểm SB, J là trung điểm SD \(\Rightarrow IJ\) là đường trung bình tam giác SBD \(\Rightarrow IJ//BD\)
Mà \(BD\perp\left(SAC\right)\) (cmt câu b) \(\Rightarrow IJ\perp\left(SAC\right)\)
Trong \(\Delta SCD\) có IM là đường trung bình \(\Rightarrow IM//CD\Rightarrow IM//\left(ABCD\right)\)
Lại có \(\left\{{}\begin{matrix}IJ//BD\left(cmt\right)\\BD\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow IJ//\left(ABCD\right)\)
\(\Rightarrow\left(MIJ\right)//\left(ABCD\right)\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp\left(MIJ\right)\)

a/ \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\\\left(SAB\right)\cap\left(SAD\right)=SA\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
b/ \(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(tan\widehat{SBA}=\frac{SA}{AB}=2\Rightarrow\widehat{SBA}\approx63^026'\)
c/ \(AB=BC\Rightarrow\Delta ABC\) cân tại B
\(\Rightarrow\) BO là trung tuyến đồng thời là đường cao
\(\Rightarrow BO\perp AC\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BO\)
\(\Rightarrow BO\perp\left(SAC\right)\Rightarrow\left(SBO\right)\perp\left(SAC\right)\)
d/ \(AC=AB\sqrt{2}=a\sqrt{2}\)
Gọi M là trung điểm AD \(\Rightarrow AM=\frac{AD}{2}=a\Rightarrow CM=MD=a\)
\(\Rightarrow CD=CM\sqrt{2}=a\sqrt{2}\)
\(\Rightarrow CD^2+AC^2=AD^2\Rightarrow AC\perp CD\)
\(\Rightarrow\widehat{SCA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SCA}=\frac{SA}{AC}=\sqrt{2}\Rightarrow\widehat{SCA}\approx54^044'\)