TT
7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
16 tháng 7 2016
Đặt A=1/2+1/4+1/8+1/16+1/32+...+1/2048+1/4096
\(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{12}}\)
\(2A=2\left(\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{12}}\right)\)
\(2A=1+\frac{1}{2}+...+\frac{1}{2^{11}}\)
\(2A-A=\left(1+\frac{1}{2}+...+\frac{1}{2^{11}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{12}}\right)\)
\(A=1-\frac{1}{2^{12}}\)
NT
0
11 tháng 3 2015
Cái này mình làm không chắc chắn đâu nha !
10^n lúc nào chia 9 cũng dư 1(100 : 9 dư 1; 1000 chia 9 dư 1.....)
18 chia hết cho 9 => 18n chia hết cho 9
Vậy A= 10^n+18n-1 chia hết cho 9
Mà số chia hết cho 9 là chia hết cho 81 nên A chia hết cho 81
11 tháng 2 2016
chúng minh A là số chính phương mà chia hết cho 9 ý
12 tháng 10 2014
S=2+22+23+....+2100
2.S=2+(22+23+...+299+2100)
2.S=22+23+24+...+2100+2101
-S=2+22+23+24+...+2100
2.S-S=2101-2
S=2100
Lưu Ý:Những chữ số mình viết thẳng hàng hay như thế nào thì bạn trình bày y như thế mới đúng ,kể cả gạch dài nha!
S
26 tháng 7 2016
\(A< \frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+....+\frac{1}{99.100}\)
\(A< \frac{1}{4}-\frac{1}{100}\)
\(A< \frac{6}{25}< \frac{1}{4}\)
5 tháng 1 2017
1+2+4+8+16+32+64+128+256+512+1024+2048
=1+(2+8)+(4+16)+(32+128)+(64+256)+(512+2048)+1024
=1+10+20+160+320+2560+1024
=4095
5 tháng 1 2017
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 + 1024 + 2048 = 4095
k nha 
công chúa nụ cười =_= ^_^
6 tháng 11 2021
\(A=3\left(1+3+3^2\right)+...+3^{2011}\left(1+3+3^2\right)\)
\(=13\cdot\left(3+...+3^{2011}\right)⋮13\)
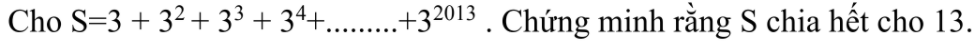
Đặt \(A=1+2+4+.........+4096\)
\(2A=2+4+8+......+8192\)
\(\Rightarrow2A-A=8192-1\)
\(\Rightarrow A=8191\)
Đặt \(S=1+2+4+...+1024+2048+4096\)
\(S=1+2^1+2^2+2^3+....+2^{10}+2^{11}+2^{12}\)
\(2S=2+2^2+2^3+....+2^{11}+2^{12}+2^{13}\)
\(2S-S=\left(2+2^2+2^3+....+2^{12}+2^{13}\right)-\left(1+2+2^2+....+2^{11}+2^{12}\right)\)
\(S=2^{13}-1=8192-1=8191\)