
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
\(S=\left\{1,\dfrac{4}{11}\right\}\)
Đặt C(x)=0
\(\Leftrightarrow11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\11x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
Vậy: Nghiệm của đa thức \(C\left(x\right)=11x^2-15x+4\) là 1 và \(\dfrac{4}{11}\)

Ta có: x+y+1=0
nên x+y=-1
Ta có: \(N=x^2\left(x+y\right)-y^2\left(x+y\right)+x^2-y^2+2\left(x+y\right)+3\)
\(=\left(x+y\right)\left(x^2-y^2\right)+\left(x^2-y^2\right)+2\left(x+y\right)+3\)
\(=\left(x^2-y^2\right)\left(x+y+1\right)+2\left(x+y\right)+3\)
\(=\left(x^2-y^2\right)\cdot0+2\cdot\left(-1\right)+3\)
=-2+3=1

Đáp án:
P=\(\frac{2}{3}\)
Giải thích các bước giải:
x:y:z=5:4:3
⇒ x5x5 =y4y4 ⇒y= 4x54x5
⇒ x5x5 =z3z3 ⇒z= 3x53x5
Thay vào biểu thức ta được:
P= x+2y−3zx−2y+3zx+2y−3zx−2y+3z= x+2.4x5−33x5x−2.4x5+33x5x+2.4x5−33x5x−2.4x5+33x5 =4x56x54x56x5 =2323
Vậy P=\(\frac{2}{3}\)
# Chúc bạn học tốt!
Vì x,y,z tỉ lệ với các số 5,4,3 nên ta có : \(x:y:z=5:4:3\) hoặc \(\frac{x}{5}=\frac{y}{4}=\frac{z}{3}\)
Ta lại có : \(\frac{x}{5}=\frac{y}{4}=\frac{z}{3}=\frac{x}{5}=\frac{2y}{8}=\frac{3z}{9}\)
Đặt \(\frac{x}{5}=\frac{2y}{8}=\frac{3z}{9}=k\Rightarrow\hept{\begin{cases}x=5k\\2y=8k\\3z=9k\end{cases}}\)
\(P=\frac{x+2y-3z}{x-2y+3z}=\frac{5k+8k-9k}{5k-8k+9k}=\frac{4k}{6k}=\frac{4}{6}=\frac{2}{3}\)
Vậy \(P=\frac{2}{3}\)
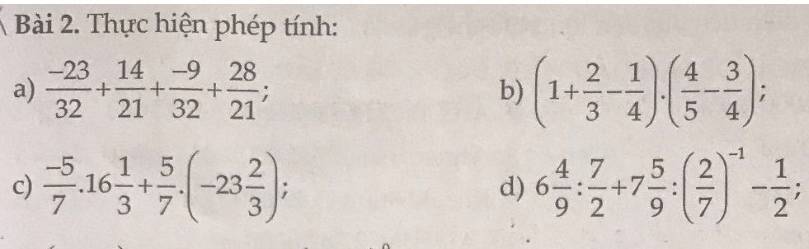
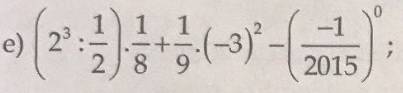
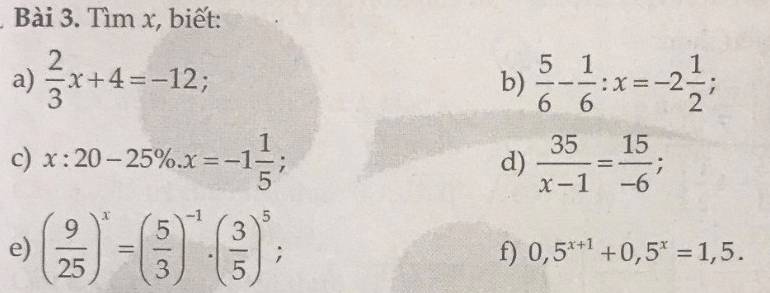
Bài 3:
a)
\(\dfrac{2}{3}x+4=-12\\ \Rightarrow\dfrac{2}{3}x=-12-4=-16\\ \Rightarrow x=-16:\dfrac{2}{3}\Rightarrow x=-24\)
b) \(\dfrac{5}{6}-\dfrac{1}{6}:x=-2\dfrac{1}{2}\)
\(\Rightarrow\dfrac{5}{6}-\dfrac{1}{6}:x=-\dfrac{3}{2}\\ \Rightarrow\dfrac{1}{6}:x=\dfrac{5}{6}+\dfrac{3}{2}\\ \Rightarrow\dfrac{1}{6}:x=\dfrac{14}{6}\\ \Rightarrow x=\dfrac{1}{6}:\dfrac{14}{6}=\dfrac{1}{14}\)
c) \(x:20-25\%x=-1\dfrac{1}{5}\)
\(\Rightarrow\dfrac{x}{20}-\dfrac{x}{4}=-\dfrac{4}{5}\)
\(\Rightarrow\dfrac{x}{20}-\dfrac{5x}{20}=-\dfrac{4}{5}\)
\(\Rightarrow-\dfrac{4x}{20}=\dfrac{-4}{5}\)
\(\Rightarrow-\dfrac{x}{5}=-\dfrac{4}{5}\)
\(\Rightarrow x=-4\)
d) \(\dfrac{35}{x-1}=\dfrac{15}{-6}\left(x\ne1\right)\)
\(\Rightarrow-6\cdot35=15\left(x-1\right)\\ \Rightarrow-210=15x-15\\ \Rightarrow15x=-210+15=-195\\ \Rightarrow x=\dfrac{-195}{15}\\ \Rightarrow x=-13\)
e)
\(\left(\dfrac{9}{25}\right)^x=\left(\dfrac{5}{3}\right)^{-1}\cdot\left(\dfrac{3}{5}\right)^5\\ \Rightarrow\left[\left(\dfrac{3}{5}\right)^2\right]^x=\dfrac{3}{5}\cdot\left(\dfrac{3}{5}\right)^5\\ \Rightarrow\left(\dfrac{3}{5}\right)^{2x}=\left(\dfrac{3}{5}\right)^6\\ \Rightarrow2x=6\\ \Rightarrow x=3\)
f)
\(0,5^{x+1}+0,5^x=1,5\\ \Rightarrow0,5^x\cdot\left(0,5+1\right)=1,5\\ \Rightarrow0,5^x\cdot1,5=1,5\\ \Rightarrow0,5^x=1,5:1,5=1\\ \Rightarrow0,5^x=0,5^0\\ \Rightarrow x=0\)
Bài 3:
a: \(\dfrac{2}{3}x+4=-12\)
=>\(\dfrac{2}{3}x=-12-4=-16\)
=>\(x=-16:\dfrac{2}{3}=-16\cdot\dfrac{3}{2}=-24\)
b: \(\dfrac{5}{6}-\dfrac{1}{6}:x=-2\dfrac{1}{2}\)
=>\(\dfrac{5}{6}-\dfrac{1}{6}:x=-\dfrac{5}{2}\)
=>\(\dfrac{1}{6}:x=\dfrac{5}{6}+\dfrac{5}{2}=\dfrac{5}{6}+\dfrac{15}{6}=\dfrac{20}{6}=\dfrac{10}{3}\)
=>\(x=\dfrac{1}{6}:\dfrac{10}{3}=\dfrac{1}{6}\cdot\dfrac{3}{10}=\dfrac{1}{20}\)
c: \(x:20-25\%\cdot x=-1\dfrac{1}{5}\)
=>\(0,05x-0,25x=-1,2\)
=>-0,2x=-1,2
=>x=1,2:0,2=6
d: \(\dfrac{35}{x-1}=\dfrac{15}{-6}\)(ĐKXĐ: \(x\ne1\))
=>\(x-1=\dfrac{35\cdot\left(-6\right)}{15}=\dfrac{-210}{15}=-14\)
=>x=-14+1=-13(nhận)
e: \(\left(\dfrac{9}{25}\right)^x=\left(\dfrac{5}{3}\right)^{-1}\cdot\left(\dfrac{3}{5}\right)^5\)
=>\(\left(\dfrac{3}{5}\right)^{2x}=\left(\dfrac{3}{5}\right)\cdot\left(\dfrac{3}{5}\right)^5=\left(\dfrac{3}{5}\right)^6\)
=>2x=6
=>x=3
f: \(0,5^{x+1}+0,5^x=1,5\)
=>\(0,5^x\cdot\left(0,5+1\right)=1,5\)
=>\(0,5^x=1\)
=>x=0
Bài 2:
a: \(\dfrac{-23}{32}+\dfrac{14}{21}+\dfrac{-9}{32}+\dfrac{28}{21}\)
\(=\left(-\dfrac{23}{32}-\dfrac{9}{32}\right)+\left(\dfrac{14}{21}+\dfrac{28}{21}\right)\)
\(=-\dfrac{32}{32}+\dfrac{42}{21}=-1+2=1\)
b: \(\left(1+\dfrac{2}{3}-\dfrac{1}{4}\right)\cdot\left(\dfrac{4}{5}-\dfrac{3}{4}\right)\)
\(=\left(\dfrac{12}{12}+\dfrac{8}{12}-\dfrac{3}{12}\right)\cdot\left(\dfrac{16}{20}-\dfrac{15}{20}\right)\)
\(=\dfrac{17}{12}\cdot\dfrac{1}{20}=\dfrac{17}{240}\)
c: \(\dfrac{-5}{7}\cdot16\dfrac{1}{3}+\dfrac{5}{7}\cdot\left(-23\dfrac{2}{3}\right)\)
\(=\dfrac{-5}{7}\cdot\left(16+\dfrac{1}{3}+23+\dfrac{2}{3}\right)\)
\(=-\dfrac{5}{7}\cdot40=-\dfrac{200}{7}\)
d: \(6\dfrac{4}{9}:\dfrac{7}{2}+7\dfrac{5}{9}:\left(\dfrac{2}{7}\right)^{-1}-\dfrac{1}{2}\)
\(=\left(6+\dfrac{4}{9}\right)\cdot\dfrac{2}{7}+\left(7+\dfrac{5}{9}\right)\cdot\dfrac{2}{7}-\dfrac{1}{2}\)
\(=\dfrac{2}{7}\left(6+\dfrac{4}{9}+7+\dfrac{5}{9}\right)-\dfrac{1}{2}=\dfrac{2}{7}\cdot14-\dfrac{1}{2}=4-\dfrac{1}{2}=\dfrac{7}{2}\)
e: \(\left(2^3:\dfrac{1}{2}\right)\cdot\dfrac{1}{8}+\dfrac{1}{9}\cdot\left(-3\right)^2-\left(-\dfrac{1}{2015}\right)^0\)
\(=\left(8\cdot2\right)\cdot\dfrac{1}{8}+\dfrac{1}{9}\cdot9-1=2+1-1=2\)