K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 3 2021
Số chính phương khi chia 3 chỉ dư 0 hoặc 1.
Trường hợp 1:
\(a^2\equiv1\left(mod3\right);b^2\equiv0\left(mod3\right)\Leftrightarrow a^2+b^2\equiv1\left(mod3\right)\)(loại)
Trường hợp 2:
\(a^2\equiv1\left(mod\right)3;b^2\equiv1\left(mod3\right)\Leftrightarrow a^2+b^2\equiv2\left(mod3\right)\)(loại)
Trường hợp 3:
\(a^2\equiv0\left(mod3\right);b^2\equiv0\left(mod3\right)\Leftrightarrow a^2+b^2\equiv0\left(mod3\right)\) ( thỏa mãn )
Vậy có đpcm.
11 tháng 3 2021
Giải:
Giả sử a không ⋮ 3 ➩ b không ⋮ 3
➩\(a^2 - 1 + b^2-1\) ⋮ 3
Mà \(a^2 +b^2\)➩2⋮ 3 (không có thể)
Vậy ➩a và b ⋮ 3.
TT
11 tháng 12 2023
P = 2.3.4....a => P chia hết cho 3
=> P - 1 : 3 dư 2 => Ko là SCP
Ta có : 3.4.....a lẻ = 2k+1 => P = 2(2k+1) = 4k + 2
=> P + 1 = 4k + 2 + 1 = 4k + 3 : 4 dư 3 => Ko là SCP
=> P - 1 và P + 1 Ko là SCP
T
3
24 tháng 3 2021
Ta có: \(S=\dfrac{4}{1\cdot3}+\dfrac{16}{3\cdot5}+\dfrac{36}{5\cdot7}+...+\dfrac{2500}{49\cdot51}\)
\(=1+\dfrac{1}{1\cdot3}+1+\dfrac{1}{3\cdot5}+1+\dfrac{1}{5\cdot7}+...+1+\dfrac{1}{49\cdot51}\)
\(=25+\dfrac{1}{2}\cdot\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{49\cdot51}\right)\)
\(=25+\dfrac{1}{2}\cdot\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=25+\dfrac{1}{2}\left(1-\dfrac{1}{51}\right)\)
\(=25+\dfrac{1}{2}\cdot\dfrac{50}{51}\)
\(=25+\dfrac{25}{51}\)
\(=25\cdot\dfrac{52}{51}=\dfrac{1300}{51}\)
DA
1
11 tháng 3 2021
Giả sử tồn tại n thoả mãn đề bài.
Dễ thấy \(2019^{2018}+1\) chẵn nên \(n^3+2018n\), suy ra n chẵn.
Do đó \(n^3+2018n⋮4\).
Mặt khác ta có \(2019^{2018}\equiv\left(-1\right)^{2018}\equiv1\left(mod4\right)\Rightarrow2019^{2018}+1\equiv2\left(mod4\right)\).
Điều này là vô lí vì VT chia hết cho 4 còn VP không chia hết cho 4.
Vậy không tồn tại n thoả mãn đề bài.
NT
4
6 tháng 5 2022
-8/12 rút gọn bằng-2/3; 15/-60 =-1/4; -16/-72=2/9;35/14.15=1/6
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 12 2023
Phần bể chưa có nước bằng:
1 - \(\dfrac{1}{4}\) = \(\dfrac{3}{4}\) (thể tích bể)
Bể sẽ đầy sau:
\(\dfrac{3}{4}\) : \(\dfrac{1}{8}\) = 6 (giờ)
Đs...
HH
1
T
3 tháng 6 2022
Ta có : p8n+3p4n- 4 = (p4n)2+3p4n- 4
Vì p là số nguyên tố lớn hơn 5 nên p có tận cùng là chữ số 1;3;7 hoặc 9
+) Với p = (...1), ta có: p4n=(...1)4n=(...1)
=> (p4n)2=(...1)2=(...1); 3p4n= 3.(...1)=(...3)
=>(p4n)2+3p4n- 4=(...1)+(...3)-4=(...0) chia hết cho 5
+) Với p = (...3), ta có: p4n=(...3)4n=(...1)
=> (p4n)2=(...1)2=(...1); 3p4n= 3.(...1)=(...3)
=>(p4n)2+3p4n- 4=(...1)+(...3)-4=(...0) chia hết cho 5
+) Với p = (...7), ta có: p4n=(...7)4n=(...1)
=> (p4n)2=(...1)2=(...1); 3p4n= 3.(...1)=(...3)
=>(p4n)2+3p4n- 4=(...1)+(...3)-4=(...0) chia hết cho 5
+) Với p = (...9), ta có: p4n=[(...9)2n]2=(...1)2=(...1)
=> (p4n)2=(...1)2=(...1); 3p4n= 3.(...1)=(...3)
=>(p4n)2+3p4n- 4=(...1)+(...3)-4=(...0) chia hết cho 5
Vậy p8n+3p4n- 4 chia hết cho 5 khi p là số nguyên tố lớn hơn 5
20 tháng 2 2021
a + 3 ≤x≤a + 2018 ( a ∈N )
vậy x thuộc (a+3;a+4;a+5;a+6;...;a+2018)
tổng:
a+3+a+4+a+5+a+6+a+7+...+a+2018
=a*2016+3+4+5+6+7+...+2018
=a*2016+(2018+3)*2016:2
-----đến đây cậu làm đc ùi-mik lười lắm ------
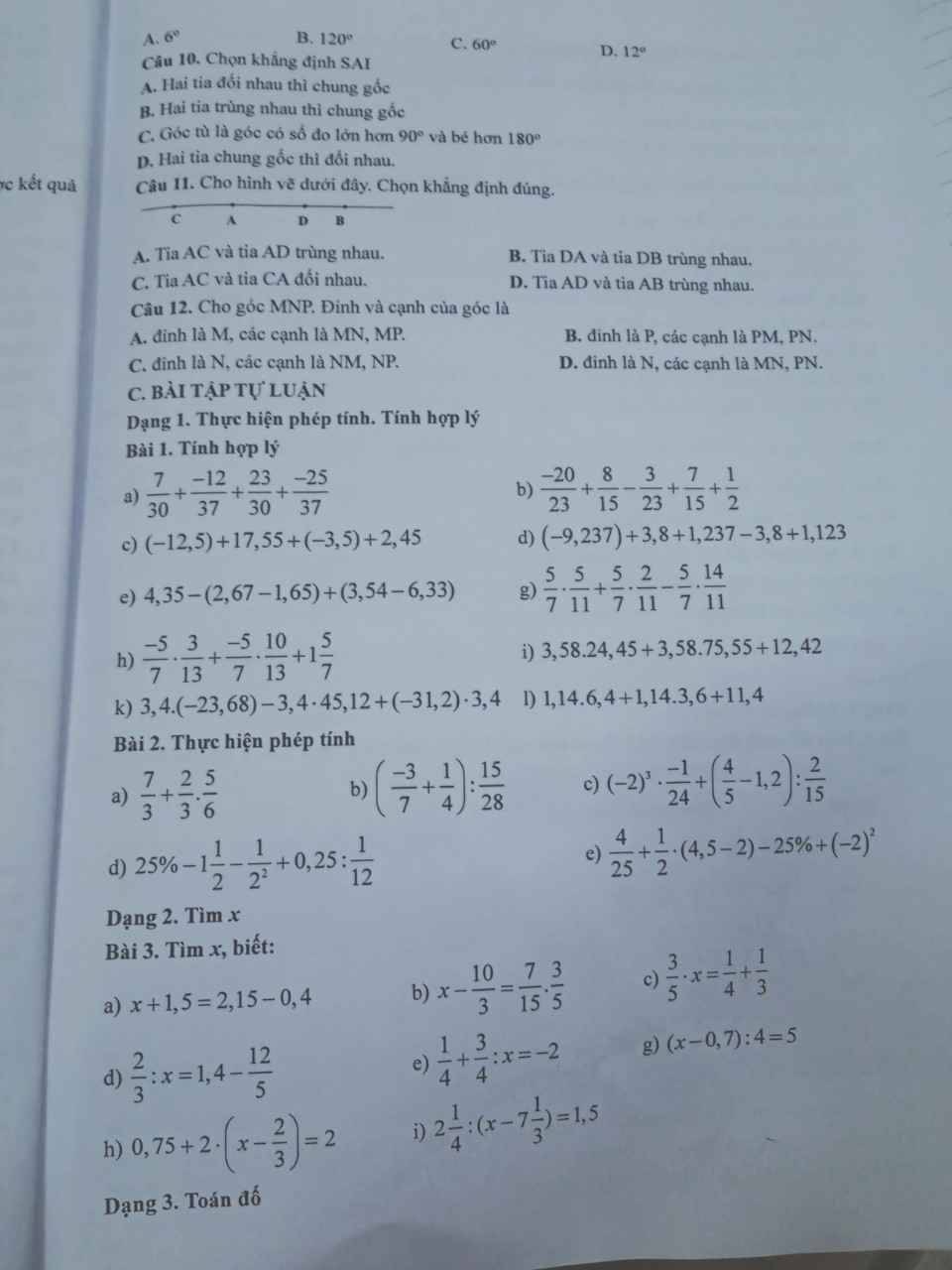
Câu 1: B
Câu 2: D
Câu 3: B
Câu 4: C
Câu 5: A
Câu 6: B
Câu 7: C
Câu 8: B
Câu 9: C
Câu 10: D
Câu 11: D
Câu 12: C
Bài 1:
a: \(\dfrac{7}{30}+\dfrac{-12}{37}+\dfrac{23}{30}+\dfrac{-25}{37}\)
\(=\left(\dfrac{7}{30}+\dfrac{23}{30}\right)+\left(-\dfrac{12}{37}-\dfrac{25}{37}\right)\)
\(=\dfrac{30}{30}+\dfrac{-37}{37}=1-1=0\)
b: \(\dfrac{-20}{23}+\dfrac{8}{15}-\dfrac{3}{23}+\dfrac{7}{15}+\dfrac{1}{2}\)
\(=\left(-\dfrac{20}{23}-\dfrac{3}{23}\right)+\left(\dfrac{8}{15}+\dfrac{7}{15}\right)+\dfrac{1}{2}\)
\(=-1+1+\dfrac{1}{2}=\dfrac{1}{2}\)
c: \(\left(-12,5\right)+17,55+\left(-3,5\right)+2,45\)
\(=\left(-12,5-3,5\right)+\left(17,55+2,45\right)\)
=20-16
=4
d: \(\left(-9,237\right)+3,8+1,237-3,8+1,123\)
\(=\left(-9,237+1,237\right)+\left(3,8-3,8\right)+1,123\)
=-8+1,123
=-6,877
e: \(4,35-\left(2,67-1,65\right)+\left(3,54-6,33\right)\)
\(=4,35-2,67+1,65+3,54-6,33\)
\(=6-9+3,54=3,54-3=0,54\)
g: \(\dfrac{5}{7}\cdot\dfrac{5}{11}+\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{14}{11}\)
\(=\dfrac{5}{7}\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)=\dfrac{5}{7}\cdot\dfrac{-7}{11}=-\dfrac{5}{11}\)
h: \(\dfrac{-5}{7}\cdot\dfrac{3}{13}+\dfrac{-5}{7}\cdot\dfrac{10}{13}+1\dfrac{5}{7}\)
\(=-\dfrac{5}{7}\left(\dfrac{3}{13}+\dfrac{10}{13}\right)+\dfrac{12}{7}=-\dfrac{5}{7}+\dfrac{12}{7}=\dfrac{7}{7}=1\)
i: \(3,58\cdot24,45+3,58\cdot75,55+12,42\)
\(=3,58\left(24,45+75,55\right)+12,42\)
\(=358+12,42=370,42\)
k: \(3,4\cdot\left(-23,68\right)-3,4\cdot45,12+\left(-31,2\right)\cdot3,4\)
\(=3,4\left(-23,68-45,12-31,2\right)\)
\(=3,4\cdot\left(-100\right)=-340\)
l: \(1,14\cdot6,4+1,14\cdot3,6+11,4\)
\(=1,14\left(6,4+3,6\right)+1,14\cdot10\)
\(=1,14\cdot20=22,8\)
Giúp mk với!