K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MN
20 tháng 2 2021
\(11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
\(S=\left\{1,\dfrac{4}{11}\right\}\)
20 tháng 2 2021
Đặt C(x)=0
\(\Leftrightarrow11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\11x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
Vậy: Nghiệm của đa thức \(C\left(x\right)=11x^2-15x+4\) là 1 và \(\dfrac{4}{11}\)
HR
2
31 tháng 3 2021
Ta có: x+y+1=0
nên x+y=-1
Ta có: \(N=x^2\left(x+y\right)-y^2\left(x+y\right)+x^2-y^2+2\left(x+y\right)+3\)
\(=\left(x+y\right)\left(x^2-y^2\right)+\left(x^2-y^2\right)+2\left(x+y\right)+3\)
\(=\left(x^2-y^2\right)\left(x+y+1\right)+2\left(x+y\right)+3\)
\(=\left(x^2-y^2\right)\cdot0+2\cdot\left(-1\right)+3\)
=-2+3=1
HQ
2
13 tháng 12 2020
Đáp án:
P=\(\frac{2}{3}\)
Giải thích các bước giải:
x:y:z=5:4:3
⇒ x5x5 =y4y4 ⇒y= 4x54x5
⇒ x5x5 =z3z3 ⇒z= 3x53x5
Thay vào biểu thức ta được:
P= x+2y−3zx−2y+3zx+2y−3zx−2y+3z= x+2.4x5−33x5x−2.4x5+33x5x+2.4x5−33x5x−2.4x5+33x5 =4x56x54x56x5 =2323
Vậy P=\(\frac{2}{3}\)
# Chúc bạn học tốt!
13 tháng 12 2020
Vì x,y,z tỉ lệ với các số 5,4,3 nên ta có : \(x:y:z=5:4:3\) hoặc \(\frac{x}{5}=\frac{y}{4}=\frac{z}{3}\)
Ta lại có : \(\frac{x}{5}=\frac{y}{4}=\frac{z}{3}=\frac{x}{5}=\frac{2y}{8}=\frac{3z}{9}\)
Đặt \(\frac{x}{5}=\frac{2y}{8}=\frac{3z}{9}=k\Rightarrow\hept{\begin{cases}x=5k\\2y=8k\\3z=9k\end{cases}}\)
\(P=\frac{x+2y-3z}{x-2y+3z}=\frac{5k+8k-9k}{5k-8k+9k}=\frac{4k}{6k}=\frac{4}{6}=\frac{2}{3}\)
Vậy \(P=\frac{2}{3}\)
NT
1
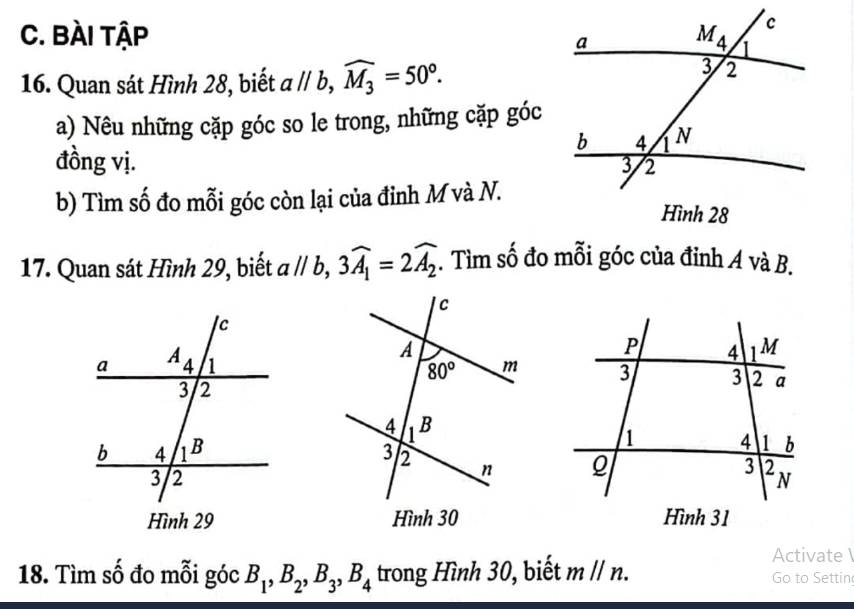
`@` `\text {Ans}`
`\downarrow`
`16,`
`@` Các cặp góc đồng vị:
`+`\(\widehat {M_4}\) và \(\widehat {N_4}\)
`+`\(\widehat {M_1}\) và \(\widehat {N_1}\)
`+`\(\widehat {M_2}\) và \(\widehat {N_2}\)
`+`\(\widehat {M_3}\) và \(\widehat {N_3}\)
`@` Các cặp góc sole trong:
`+`\(\widehat {M_3} \) và \(\widehat {N_1}\)
`+`\(\widehat {M_2}\) và \(\widehat {N_4}\)
`b,`
Ta có: \(\widehat {M_3} = \widehat {M_1} (\text {đối đỉnh})\)
`=>`\(\widehat {M_1}=50^0\)
\(\widehat {M_3}+\widehat {M_2}=180^0 (\text {kề bù})\)
`=>`\(50^0+\widehat {M_2}=180^0\)
`=>`\(\widehat {M_2}=180^0-50^0=130^0\)
\(\widehat {M_2}=\widehat {M_4} (\text {2 góc đối đỉnh})\)
`=>`\(\widehat {M_4} = 130^0\)
Vì \(\widehat {M_3}\) và \(\widehat {N_1}\) là `2` góc sole trong
`=>`\(\widehat {M_3}=\widehat {N_1}=50^0\)
\(\widehat {M_3}=\widehat {N_3}=50^0 (\text {2 góc đồng vị})\)
\(\widehat {M_2}=\widehat {N_2}=130^0 (\text {2 góc đồng vị})\)
\(\widehat {M_2}=\widehat {N_4}=130^0 (\text {2 góc slt})\)
`17,`
Vì \(\widehat {A_1}\) và \(\widehat {A_2}\) là `2` góc kề bù
`=>`\(\widehat {A_1}+\widehat {A_2}=180^0\)
\(3\widehat {A_1}=2\widehat {A_2}\) (gt)
`=>`\(\widehat{A_1}=\dfrac{2}{3}\cdot\widehat{A_2}\)
Thay \(\widehat{A_1}=\dfrac{2}{3}\widehat{A_2}\)
\(\dfrac{2}{3}\cdot\widehat{A_2}+\widehat{A_2}=180^0\)
`=>`\(\widehat{A_2}\left(\dfrac{2}{3}+1\right)=180^0\)
`=>`\(\widehat{A_2}\cdot\dfrac{5}{3}=180^0\)
`=>`\(\widehat{A_2}=180^0\div\dfrac{5}{3}\)
`=>`\(\widehat{A_2}=108^0\)
Vậy, số đo \(\widehat{A_2}=108^0\)
\(\widehat {A_1}+\widehat {A_2}=180^0 (\text {kề bù})\)
`=>`\(\widehat{A_1}+108^0=180^0\)
`=>`\(\widehat{A_1}=72^0\)
\(\widehat {A_1}=\widehat {A_3}=72^0 (\text {đối đỉnh})\)
\(\widehat {A_2}=\widehat {A_4}=108^0 (\text {đối đỉnh})\)
`@` Số đo các góc của đỉnh B:
`+`\(\widehat {A_4}=\widehat {B_4}=108^0 (\text {đồng vị})\)
`+`\(\widehat {A_2}=\widehat {B_2}=108^0 (\text {đồng vị})\)
`+`\(\widehat {A_3}=\widehat {B_1}=72^0 (\text {sole trong})\)
`+`\(\widehat {A_3}=\widehat {B_3}=72^0 (\text {đồng vị})\)