Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

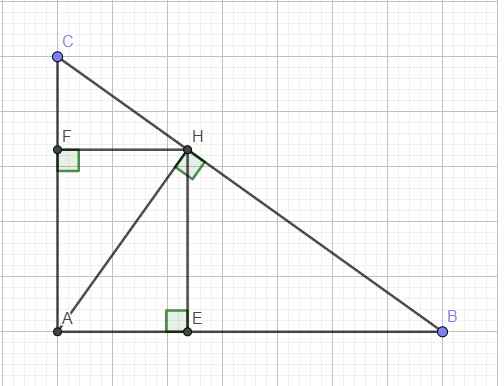
Tứ giác AEHF là hình chữ nhật (có 3 góc vuông) \(\Rightarrow HE=AF\)
Áp dụng định lý Pitago trong tam giác vuông AFH:
\(AH^2=AF^2+HF^2=HE^2+HF^2\)
Áp dụng hệ thức lượng trong tam giác vuông AHB với đường cao HF:
\(HF^2=AF.FC\)
Tương tự:
\(HE^2=AE.EB\)
\(\Rightarrow AH^2=HE^2+HF^2=AE.EB+AF.FC\) (đpcm)

Cho tam giác ABC vuông tại A( AB<AC ), có đường cao AH, trung tuyến AM Gọi E và F lần lượt la hình chiếu của H lên AB và AC; I và K lần lượt là trung điểm của HB và HC. CM :

Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

a:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=10^2-6^2=64\)
hay AC=8
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8cm

a) tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=81\Rightarrow AB=9\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.9}{15}=\dfrac{36}{5}\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=\dfrac{27}{5}\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=\dfrac{48}{5}\left(cm\right)\)
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHC vuông tại HA có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AC=AH^2=AE.AB\)
c) Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow AH=EF\)
tam giác EHF vuông tại H nên áp dụng Py-ta-go
\(\Rightarrow HE^2+HF^2=EF^2=AH^2\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=HB.HC\Rightarrow HE^2+HF^2=HB.HC\)

a, Áp dụng HTL: \(\left\{{}\begin{matrix}BC=\dfrac{AB^2}{BH}=20\left(cm\right)\\AC=\sqrt{BC^2-AB^2}=10\sqrt{3}\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=5\sqrt{3}\left(cm\right)\end{matrix}\right.\)
b, Vì \(\widehat{AFH}=\widehat{AEH}=\widehat{FAE}=90^0\) nên AFHE là hcn
Do đó \(AF=HE\)
Áp dụng HTL: \(AE\cdot EB=EH^2\Rightarrow AE\cdot EB=AF^2\)

b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AF=HE(1)
Xét ΔAHB vuông tại H có HE là đường cao
nên \(EA\cdot EB=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot EB=AF^2\)

b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AF=HE(1)
Xét ΔAHB vuông tại H có HE là đường cao
nên \(EA\cdot EB=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot EB=AF^2\)