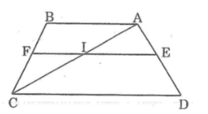
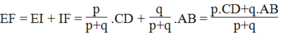Cho hình thang ABCD( AB//CD), AB=14cm, CD=35cm, AD =17,5cm. Trên AD lấy E sao cho DE =5cm. Qua E vẽ đường thẳng // AB cắt BC tại F. Tính EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 1 2018
( Mk vẽ hình có đẹp không ???? )
Gọi giao điểm của AD và BC là O
Gọi giao điểm của AC với EF là I
Xét tam giác OEF có :
AB // EF
Áp dụng định lý Ta-let , ta có :
\(\dfrac{OA}{AE}=\dfrac{OB}{BF}=>\dfrac{BF}{AE}=\dfrac{OB}{OA}\) ( 1)
Tương tự , ta có : \(\dfrac{OA}{AD}=\dfrac{OB}{BC}=>\dfrac{BC}{AD}=\dfrac{OB}{OA}\) ( 2)
Từ ( 1 ; 2) => \(\dfrac{BF}{AE}=\dfrac{BC}{AD}=>\dfrac{AE}{AD}=\dfrac{BF}{BC}=\dfrac{17,5-5}{17,5}=\dfrac{5}{7}\)
Xét tam giác ADC có :
EI //DC ( Do : EI // AB mà : AB//DC)
Áp dụng hệ quả định lý Ta-lét , ta có :
\(\dfrac{EI}{DC}=\dfrac{AE}{AD}=>EI=\dfrac{DC.AE}{AD}=\dfrac{35.12,5}{7}=62,5cm\)
Tương tự , ta có : \(\dfrac{IF}{AB}=\dfrac{CI}{AC}\)
Xét tam giác ADC có :
EI //DC ( Do : EI // AB mà : AB//DC)
Áp dụng định lý Ta-lét , ta có :
\(\dfrac{DE}{AD}=\dfrac{IC}{AC}=\dfrac{2}{7}\)
Lại có : \(\dfrac{IF}{AB}=\dfrac{CI}{AC}=>IF=\dfrac{AB.CI}{AC}=4cm\)
=> EF = EI + IF = 4 + 62,5 = 66,5 cm
19 tháng 2 2017
Gọi I là giao của EF và BD.
Vì EF//AB, áp dụng ta-lét vào tam giác DAB,ta có:\(\frac{EI}{AB}=\frac{ED}{DA}=\frac{5}{17.5}=\frac{DI}{BD}\)(1)
Vì IF//DC ,áp dụng Ta-lét vào tam giác BDC,ta có :\(\frac{DC}{IF}=\frac{DB}{IB}\)(2)
Từ (1),(2) \(\Rightarrow\)\(\frac{DI}{DB}.\frac{DB}{IB}=\frac{DI}{IB}=\frac{5}{12.5}\)
\(\Rightarrow\)\(\frac{DC}{IF}.\frac{5}{17.5}=\frac{5}{12.5}\Rightarrow\frac{IF}{DC}=\frac{12.5}{17.5}\)
Mà DC=35\(\Rightarrow\)IF =\(\frac{12.5}{17.5}\)\(\times\)35=25.
Từ (1)vì AB=14\(\Rightarrow\)EI=\(\frac{5}{17.5}\times14\)=4
Vậy IF+IE=25+4=29.
NN
10 tháng 11 2018
Xét hình thang ABCD có :
E là trung điểm của AD
EF//AB//CD (Vì EF vàCD cùng // với AB )
=) EF là đường trung bình cua hình thang ABCD
=) EF= (AB+CD):2
Thay số vào biểu thức trên ta được :
35=(15+CD) :2
15+CD=35.2
15+CD=70
CD= 70-15
CD= 55 (cm)
Vậy CD=55 cm
CM
14 tháng 10 2019
Kẻ đường chéo AC cắt EF tại I
Trong ΔADC, ta có: EI // CD
Suy ra: 
Suy ra: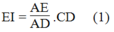 
Lại có :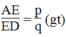 
Suy ra: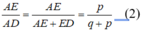 
Từ (1) và (2) suy ra: 
Trong ΔABC, ta có: FI // AB
Suy ra: 
(định lí ta-lét) (3)
Trong ΔADC, ta có : EI // CD
Suy ra: 
(định lí ta-lét) (4)
Từ (3) và (4) suy ra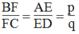 
Trong ΔABC, ta có: IF // AB
Suy ra: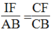 
(định lí ta-lét)
Suy ra: 
Ta có: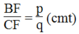 
Suy ra: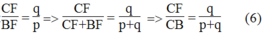 
Từ (5) và (6) suy ra: 
Vậy: 