Cho đoạn AB, I là trung điểm của AB. Qua B vẽ xy (AB không trùng với xy); vẽ AH vuông góc với xy; vẽ BK vuông góc với xy. Chứng minh AH=BK.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 4 2023
Gọi số điểm lấy thêm là x
Theo đề, ta có: \(C^2_{x+4}=351\)
=>\(\dfrac{\left(x+4\right)!}{\left(x+4-2\right)!\cdot2!}=351\)
=>(x+4)(x+3)=351*2=702
=>x^2+7x+12-702=0
=>x^2+7x-690=0
=>x=23
26 tháng 8 2021
Đường thẳng xy là đường trung trực của đoạn thẳng AB thì:
A. Đường thẳng xy vuông góc với đoạn thẳng AB tại I và I là trung điểm của đoạn AB.
B. Đường thẳng xy vuông góc với đoạn thẳng AB.
C. Đường thẳng xy đi qua trung điểm của đoạn thẳng AB
D. Đường thẳng xy vuông góc với đoạn thẳng AB tại A .
11 tháng 4 2022
a ) Vì C là trung điểm của AB
=> BC = AB / 2 = 6 / 2 = 3 cm
Vì D là trung điểm của BC
=> CD = BC / 2 = 3 / 2 = 1,5 cm
Vì AC và AD là 2 tia đối nhau
nên C nằm giữa A và D
=> AC + CD = AD
=> AD = 3 +1,5 = 4,5 cm
Vậy AD = 4,5 cm
11 tháng 4 2022
Nếu bạn thấy chỗ nào chx hiểu để mình làm lại cho dễ hiểu hơn
KN
11 tháng 4 2023
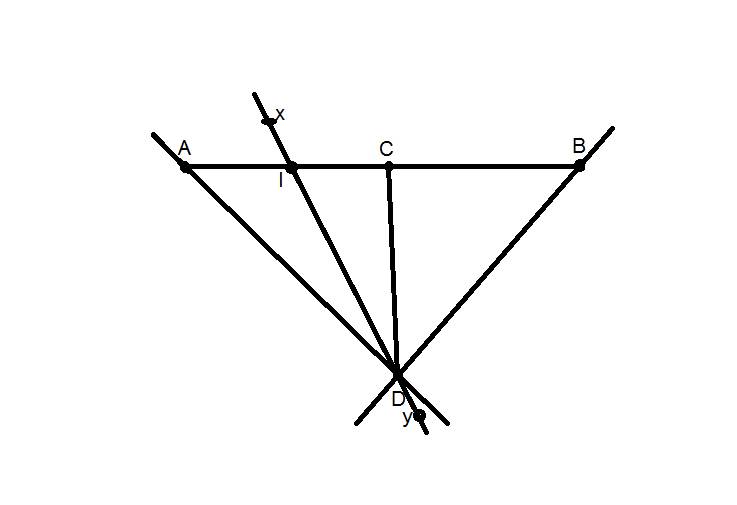
a) các tia đối nhau có gốc là I:
-AI với IC
-xI với Iy
-xI với ID
các tia trùng nhau có gốc I là:
- IC trùng với IB
- ID trùng với Iy
b) các góc đỉnh D là:
-AID,ADx, xDC, IDC, CDB, ADC,xDB,IDB, ADB
PA
7 tháng 7 2016
1) đường thẳng xy là đường trung trực của đoạn thẳng AB nếu
a) xy vuông góc AB
b) xy vuông góc với AB hoặc tại A hoặc tại B
c) xy đy qua trung điểm của AB
d) xy vuông góc với AB và đi qua trung điểm của AB
7 tháng 7 2016
1) đường thẳng xy là đường trung trực của đoạn thẳng AB nếu
a) xy vuông góc AB
b) xy vuông góc với AB hoặc tại A hoặc tại B
c) xy đy qua trung điểm của AB
d) xy vuông góc với AB và đy qua trung điểm của AB