Cho Δ ABC vuuong tại A (AB<AC),đường cao AH.Gọi D là điểm đối xứng A qua H. Trên tia HC lấy điểm M sao cho HM=HB. Gọi N là giao diểm của DM và AC.
1)CMR tứ giác ABDM là hình thoi;
2)CMR AM ⊥ CD
3)Gọi I là trung điểm của MC. CMR IN⊥ HN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GK
1
28 tháng 4 2023
a: Xet ΔAHN và ΔCHM có
AH=CH
góc HAN=góc HCM
AN=CM
=>ΔAHN=ΔCHM
b: Xet ΔAHM và ΔBHN co
AH=BH
góc HAM=góc HBN
AM=BN
=>ΔAHM=ΔBHN
PT
1
24 tháng 3 2021
a) Xét ΔCBA vuông tại A và ΔABK vuông tại K có
\(\widehat{ABK}\) chung
Do đó: ΔCBA\(\sim\)ΔABK(g-g)
CM
4 tháng 1 2018
Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 52 - 32 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/( DB + DC ) = AB /( AB + AC )
hay DB/5 = 3/( 3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.
CM
30 tháng 11 2018
Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 5 2 - 3 2 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/(DB + DC) = AB/(AB + AC)
hay DB/5 = 3/(3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.
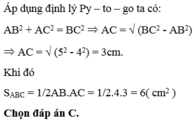
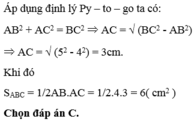
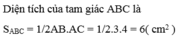
Bn ơi, bn vẽ đc hình chưa?Cho mk xem hình bn vẽ nào.