GK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
1
19 tháng 8 2017
Vẽ đường cao CH. Ta có:
\(\hept{\begin{cases}BH+AH=14\\BH^2+CH^2=225\\AH^2+CH^2=169\end{cases}\Rightarrow\hept{\begin{cases}BH+AH=14\\BH^2-AH^2=56\end{cases}\Leftrightarrow}\hept{\begin{cases}BH+AH=14\\\left(BH+AH\right)\left(BH-AH\right)=56\end{cases}\Leftrightarrow}\hept{\begin{cases}BH+AH=14\\BH-AH=4\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}BH=9\\AH=5\end{cases}\Rightarrow\hept{\begin{cases}\widehat{A}=cos^{-1}\frac{5}{13}\approx67^023'\\\widehat{B}=cos^{-1}\frac{9}{15}\approx53^08'\\\widehat{C}\approx180^0-\left(67^023'+53^08'\right)=59^029'\end{cases}}}\)
5 tháng 2 2022
a: BC=13cm
Xét ΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}=\dfrac{5}{13}\)
nên \(\widehat{C}=23^0\)
=>\(\widehat{B}=67^0\)
b: Xét ΔBAC có AE là đường phân giác
nên \(\dfrac{BE}{AB}=\dfrac{CE}{AC}\)
hay \(\dfrac{BE}{5}=\dfrac{CE}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BE}{5}=\dfrac{CE}{12}=\dfrac{BE+CE}{5+12}=\dfrac{13}{17}\)
Do đó: BE=65/17; CE=156/17
c: Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
Do đó: AMEN là hình chữ nhật
mà AE là đường phân giác
nên AMEN là hình vuông
KL
9 tháng 7 2016
Áp dụng định lí Pi ta go vào tam giác vuông AHB ta có
\(AB^2=AH^2+BH^2\) =>\(BH^2=AB^2-AH^2\)=>\(BH=\sqrt{30^2-24^2}=\sqrt{324}=18\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có
\(AH^2=BH.CH\)=>\(HC=\frac{AH^2}{BH}\)=>\(HC=\frac{24^2}{18}=\frac{576}{18}=32\left(cm\right)\)
Ta có \(BC=HC+HB\) => \(BC=32+18=50\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có
\(AC^2=BC.HC\)
=>\(AC=\sqrt{BC.HC}=\sqrt{50.32}=\sqrt{1600}=40\left(cm\right)\)*Chỗ này bạn dùng Pitago tính cũng được nha*
KL
9 tháng 7 2016
Ta có góc HBD+ góc ABH = 90 độ mà góc ACH + góc ABH = 90 độ
=> góc HBD = góc ACH
Xét tam giác BHD và tam giác CHA có
góc BHD = góc CHA = 90 độ
góc HBD = góc ACH (chứng minh trên)
Do đó tam giác BHD ~ tam giác CHA
=> \(\frac{BD}{BH}=\frac{AC}{HC}\)
=>\(BD=\frac{AC.BH}{HC}=\frac{18.40}{32}=\frac{720}{32}=22,5\left(cm\right)\)
4 tháng 10 2021
a: \(AC=BC\cdot\sin\widehat{B}=60\cdot\dfrac{1}{2}=30\left(cm\right)\)
\(AB=\sqrt{60^2-30^2}=30\sqrt{3}\)
b: \(AC=BC\cdot\cos\widehat{C}=106\cdot\dfrac{1}{2}=53\left(cm\right)\)
\(AB=\sqrt{106^2-53^2}=53\sqrt{3}\left(cm\right)\)
19 tháng 10 2021
Xét ΔABC vuông tại A có AH là đường cao
nên \(AC^2=CH\cdot BC\)
hay \(BC=\dfrac{256}{13}\left(cm\right)\)
\(\Leftrightarrow BH=\dfrac{87}{13}\left(cm\right)\)
\(\Leftrightarrow AH=\sqrt{87}\left(cm\right)\)
\(\Leftrightarrow S_{ABC}=\dfrac{BC\cdot AH}{2}=\dfrac{\sqrt{87}\cdot\dfrac{256}{13}}{2}=\dfrac{128\sqrt{87}}{13}\left(cm^2\right)\)
N
2
2 tháng 6 2021
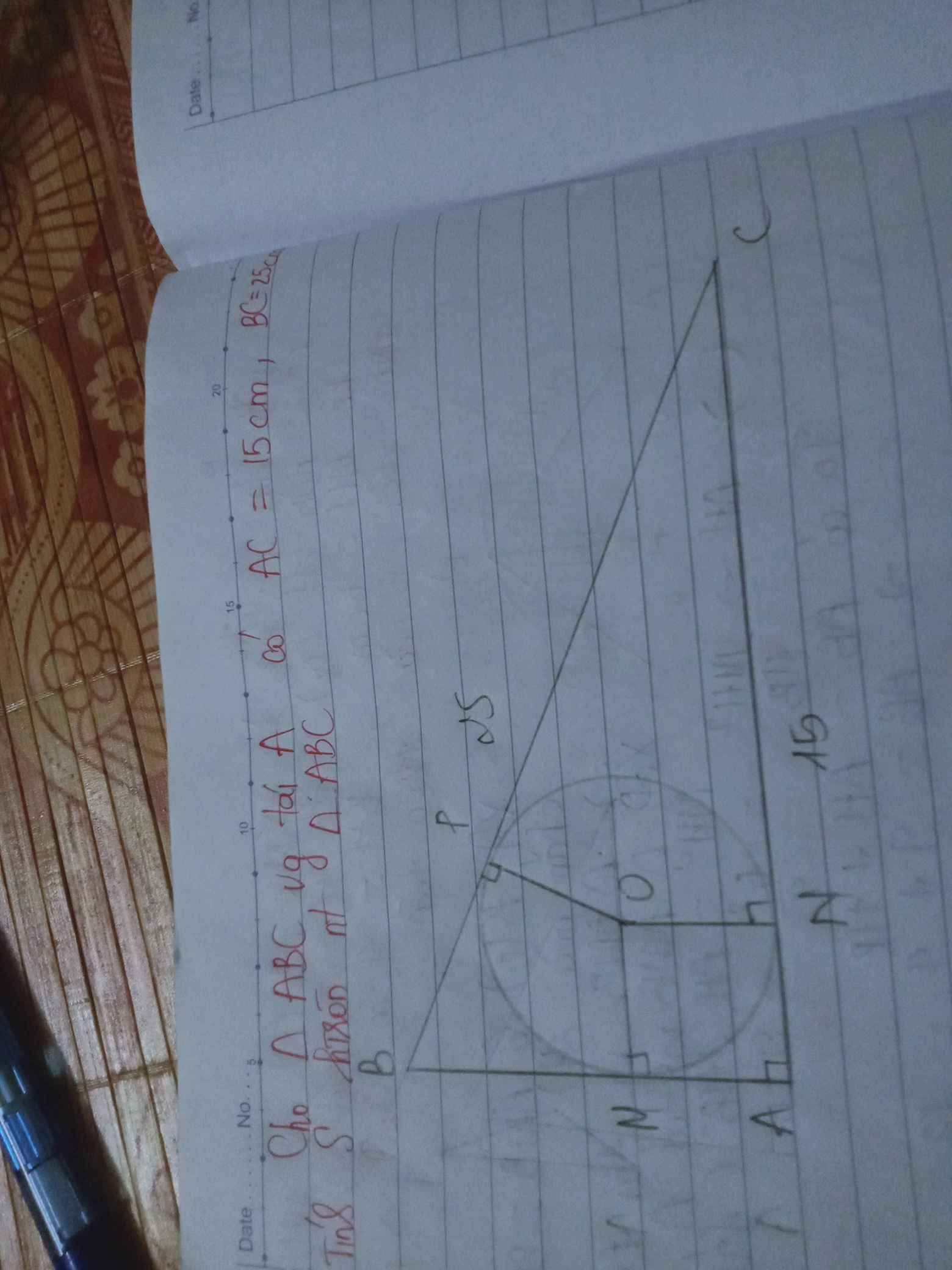
như hình vẽ trên
xét tam giác ABC vuông tại A
=>\(AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-15^2}=20cm\)
nửa chu vi tam giác ABC : \(p=\dfrac{AB+AC+BC}{2}=\dfrac{15+25+20}{2}=30cm\)
diện tích tam giác ABC : \(S=\dfrac{AB.AC}{2}=\dfrac{20.15}{2}=150cm^2\)
bán kính đường tròn nội tiếp: \(R=\dfrac{S}{p}=\dfrac{150}{30}=5cm\)
=> diện tích hình tròn nt tam giác ABC:
\(S1=\pi,R^2=3,14.5^2=78,5cm^2\)
Đề sai rồi bạn
Quên k phải là tam giác vuông