Cho tam giác ABC vuông tại A , đường phân giác AD . Gọi M,N theo thứ tự là chân các đường vuông góc kẻ từ D đến AB,AC . AMDN là hình gì ? Vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2022
Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
mà AD là tia phân giác
nên AMDN là hình vuông
DT
29 tháng 1 2016
bạn tự vẽ hình nk.
cm: vì m, n lần lượt là chân đg vuông góc kẻ từ d dến ab,ac
=> tứ giác AMDN là hình chữ nhật (có 3 góc vuông) (dh nb hcn)
mặt #: ad là đg phân giác của góc a
=> hcn AMDN là hình vuông vì có có đường chéo là đường phân giác của góc a(dh nb hv)
CM
19 tháng 12 2017
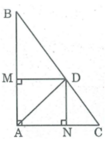
Xét tứ giác AMDN, ta có: ∠ (MAN) = 90 0 (gt)
DM ⊥ AB (gt)
⇒ ∠ (AMD) = 90 0
DN ⊥ AC (gt) ⇒ ∠ (AND) = 90 0
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông
Vì M, N là chân đường vuông góc kẻ từ D đến AB, AC =>tứ giác AMDN là hình chữ nhật (có 3 góc vuông).
(gt) =>AMDN là hình chữ nhật.
(gt) =>AMDN là hình vuông(đpcm).
29 tháng 12 2023
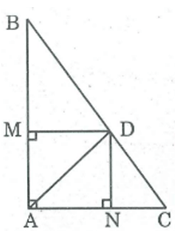
a: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{30}=\dfrac{CD}{40}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=50cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{50}{7}\)
=>\(BD=3\cdot\dfrac{50}{7}=\dfrac{150}{7}\left(cm\right);CD=4\cdot\dfrac{50}{7}=\dfrac{200}{7}\left(cm\right)\)
b: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
=>AMDN là hình chữ nhật
Hình chữ nhật AMDN có AD là phân giác của góc MAN
nên AMDN là hình vuông
C
29 tháng 10 2021
Xét tứ giác AMDN, ta có: ∠∠(MAN) = 900900 (gt)
DM ⊥ AB (gt)
⇒∠∠(AMD) = 900900
DN ⊥ AC (gt) ⇒∠∠(AND) = 900900
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông
chịu mình mới lớp 6
sorry
Tứ giác AMDN là hình chữ nhật vì có 3 góc vuông
Mặt khác ta thấy AD là tia phân giác của góc A nên suy ra AMDN là hình vuông