Công thức tính diện tích tam giác bằng đường phân giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho tam giác ABC với đường cao AH. Ta dựng hình chữ nhật có một cạnh bằng một cạnh của tam giác ABC và có diện tích bằng diện tích tam giác ABC như hình dưới
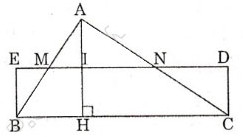
Ta có ∆EBM = ∆KAM và ∆DCN = ∆ KAN
Suy ra
SBCDE = SABC=  BC. AH
BC. AH
Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác.

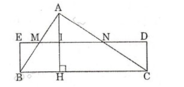
Cho ΔABC với đường cao AH.
Gọi M, N, I là trung điểm của AB, AC, AH.
Lấy E đối xứng với I qua M, D đối xứng với I qua N.
⇒ Hình chữ nhật BEDC là hình cần dựng.
Thật vậy:
Ta có ΔEBM = ΔIAM và ΔDCN = ΔIAN
⇒ SEBM = SAMI và SCND = SAIN
⇒ SABC = SAMI + SAIN + SBMNC = SEBM + SBMNC + SCND = SBCDE.
Suy ra SABC = SBCDE = BE.BC = 1/2.AH.BC. (Vì BE = IA = AH/2).
Ta đã tìm lại công thức tính diện tích tam giác bằng một phương pháp khác

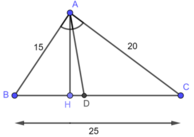
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)

Bài giải
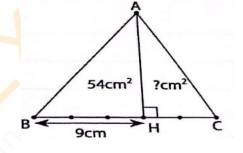
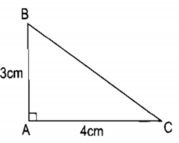
Diện tích hình tam giác đó là :
4 x 3 : 2 = 6 ( cm2 )
Đ/s : 6 cm2 .


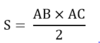
Công thức 1: Đường phân giác trong là AD:
AD = 2/ (b + c) . căn bcp (p - a)
Công thức 2:
AD = 2bc. cosA/2 / (b + c)
Đường phân giác trong góc B và C từ đó suy ra.
Cách chứng minh công thúc 1:
Sử dụng vectơ.
theo công thức đường phân giác lớp 8 ta có DB / DC = c / b
Suy ra b.vtDB = -c.vtDC
=> b. (vtDA + vtAB) = - c. (vtDA + vtAC)
=> (b + c). vtAD = b. vtAB + c. vtAC
Bình phương hai vế có
(b+c)^2 AD^2 = 2b^2c^2 + 2bc. vtAB. vtAC
Thay vtAB.vtAC = (b^2 + c^2 - a^2) / 2 (công thức)
phân tích thành nhân tử, rút gọn có đpcm.
Cách chứng minh công thức 2:
Sử dụng diện tích:
S.ABC = S.ADB + S.ADC
bc. sinA = AD.c sinA/2 + AD.b sinA/2
2bc sinA/2 .cosA/2 = AD sinA/2 (b + c)
=> AD = 2bc.cosA/2 / (b + c)
Chú ý: Có thể dùng định lí hàm cos để tính cosA/2 thay vào công thức 2 để có công thức 1.
(vtAB là vectơ AB)
bótay.com