
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


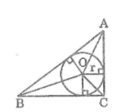
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : S A B C = S O A B + S O A C + S O B C
= (1/2).AB.r + (1/2).AC.r + (1/2).BC.r
= (1/2)(AB + AC + BC).r
Mà AB + AC + BC = 2p
Nên S A B C = (1/2).2p.r = p.r


Gọi I,E,F lần lược là tiếp điểm của đường tròn tâm O nội tiếp với AB,BC,CA ta có OI = OE = OF = r
S ABC = S AOB + S BOC + S COA = AB.OI/2 + BC.OE/2 + CA.OF/2
= (AB + BC + CA).r/2 = pr
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : SABC = SOAB + SOAC + SOBC
\(=\left(\frac{1}{2}\right)AB.r+\left(\frac{1}{2}\right).AC.r+\left(\frac{1}{2}\right).BC.r\)
\(=\left(\frac{1}{2}\right)\left(AB+AC+BC\right).r\)
Mà AB + AC + BC = 2p
Nên \(S_{ABC}=\left(\frac{1}{2}\right).2p.r=p.r\)

có cần rườm rà thế ko bn? mk chỉnh đề nhé
cho ΔABC cân tại A. trung truyến BM,CN cắt nhau tại I. CMR AI là p/g ∠BAC
vì BM và CN là 2 trung truyến của 1 Δ và cắt nhau tại I
=> I là trọng tâm ΔABC => AI là trung tuyến mà ΔABC cân tại A nên AI là p/g ∠BAC
Công thức 1: Đường phân giác trong là AD:
AD = 2/ (b + c) . căn bcp (p - a)
Công thức 2:
AD = 2bc. cosA/2 / (b + c)
Đường phân giác trong góc B và C từ đó suy ra.
Cách chứng minh công thúc 1:
Sử dụng vectơ.
theo công thức đường phân giác lớp 8 ta có DB / DC = c / b
Suy ra b.vtDB = -c.vtDC
=> b. (vtDA + vtAB) = - c. (vtDA + vtAC)
=> (b + c). vtAD = b. vtAB + c. vtAC
Bình phương hai vế có
(b+c)^2 AD^2 = 2b^2c^2 + 2bc. vtAB. vtAC
Thay vtAB.vtAC = (b^2 + c^2 - a^2) / 2 (công thức)
phân tích thành nhân tử, rút gọn có đpcm.
Cách chứng minh công thức 2:
Sử dụng diện tích:
S.ABC = S.ADB + S.ADC
bc. sinA = AD.c sinA/2 + AD.b sinA/2
2bc sinA/2 .cosA/2 = AD sinA/2 (b + c)
=> AD = 2bc.cosA/2 / (b + c)
Chú ý: Có thể dùng định lí hàm cos để tính cosA/2 thay vào công thức 2 để có công thức 1.
(vtAB là vectơ AB)
bótay.com