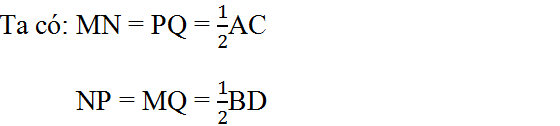Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

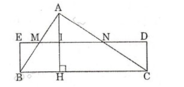
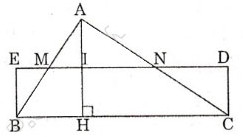
Cho ΔABC với đường cao AH.
Gọi M, N, I là trung điểm của AB, AC, AH.
Lấy E đối xứng với I qua M, D đối xứng với I qua N.
⇒ Hình chữ nhật BEDC là hình cần dựng.
Thật vậy:
Ta có ΔEBM = ΔIAM và ΔDCN = ΔIAN
⇒ SEBM = SAMI và SCND = SAIN
⇒ SABC = SAMI + SAIN + SBMNC = SEBM + SBMNC + SCND = SBCDE.
Suy ra SABC = SBCDE = BE.BC = 1/2.AH.BC. (Vì BE = IA = AH/2).
Ta đã tìm lại công thức tính diện tích tam giác bằng một phương pháp khác

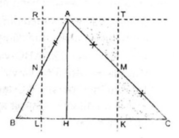
Cho tam giác ABC với đường cao AH. Ta dựng hình chữ nhật có một cạnh bằng một cạnh của tam giác ABC và có diện tích bằng diện tích tam giác ABC như hình dưới
Ta có ∆EBM = ∆KAM và ∆DCN = ∆ KAN
Suy ra
SBCDE = SABC=  BC. AH
BC. AH
Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác.

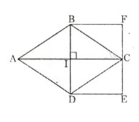
Cho hình thoi ABCD, vẽ hình chữ nhật có một cạnh là đường chéo BD, cạnh kia bằng IC (bằng nửa AC).
Khi đó diện tích của hình chữ nhật BDEF bằng diện tích hình thoi ABCD.
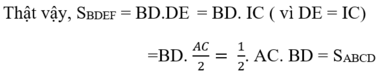
Từ đó suy ra cách tính diện tích hình thoi: Diện tích hình thoi bằng nửa tích hai đường chéo.

Cho hình thoi MNPQ, vẽ hình chữ nhật có một cạnh là đường chéo MP, cạnh kia bằng IN ( IN= NQ).
Khi đó diện tích của hình chữ nhật MPBA bằng diện tích hình thoi MNPQ.
Thật vậy SMPBA = MP. IN = MP. NQ
= MP. NQ = SMNPQ


Cho hình thoi MNPQ, vẽ hình chữ nhật có một cạnh là đường chéo MP, cạnh kia bằng IN ( IN= NQ).
Khi đó diện tích của hình chữ nhật MPBA bằng diện tích hình thoi MNPQ.
Thật vậy SMPBA = MP. IN = MP. NQ
= MP. NQ = SMNPQ
Cho hình thoi MNPQ, vẽ hình chữ nhật có một cạnh là đường chéo MP, cạnh kia bằng IN ( IN= NQ).
Khi đó diện tích của hình chữ nhật MPBA bằng diện tích hình thoi MNPQ.
Thật vậy SMPBA = MP. IN = MP. NQ
= MP. NQ = SMNPQ


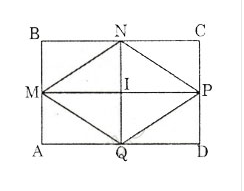
Cho hình chữ nhật ABCD; M,N,P,Q lần lượt là trung điểm của AB,BC, CD, DA.
* Chứng minh MNPQ là hình thoi
Ta có MN = PQ = 1/2BD
NP = MQ = 1/2 AC
Mà AC = BD
⇒ MN = NP = PQ = QM nên tứ giác MNPQ là hình thoi (Có 4 cạnh bằng nhau)
* Theo bài 33 (các em tham khảo ở trên), ta có SMNPQ = SABNQ và SMNPQ = SNQDC
Vì vậy SABCD = SABNQ + SNQDC = 2SMNPQ
* Ta có SABCD =2SMNPQ ⇒ SMNPQ = 1/2SABCD = 1/2AB.BC = 1/2NQ.MP
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh M, N, P, Q.
Vẽ tứ giác MNPQ
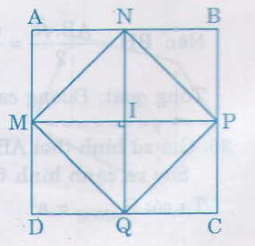
Ta có MN = PQ = \(\dfrac{1}{2}\)BD
NP = MQ = \(\dfrac{1}{2}\) AC
Mà AC = BD
Nên tứ giác MNPQ là hình thoi vì có bốn cạnh bằng nhau.
Dễ dàng chứng minh rằng : ∆AMN = ∆INM , ∆BPN = ∆NIP
∆PCQ = ∆IQP, ∆DMQ = IQM
Do đó
SMNPQ = \(\dfrac{1}{2}\) SABCD mà SABCD = AB. AD = MP. NQ
Vậy SMNPQ = \(\dfrac{1}{2}\) MP.NQ

Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
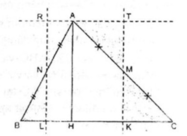
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC