3xy - x + 6y = 17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
0
AH
Akai Haruma
Giáo viên
31 tháng 12 2020
Bạn viết đề cẩn thận bằng công thức toán thì sẽ tăng khả năng nhận được sự giúp đỡ hơn. Viết như thế này nhìn rối mắt cực.
18 tháng 7 2021
Ta có:x+6y+3xy+35=0
<=> x(1+3y)+2(1+3y)+33=0
<=> (1+3y)(x+2)=-33
Do \(y\in Z\Rightarrow3y⋮3\Rightarrow1+3y\) chia 3 dư 1
Mà trong các Ư(-33) chỉ có -11 và 1 là chia 3 dư 1
TH1.\(\left\{{}\begin{matrix}1+3y=1\\x+2=-33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-35\end{matrix}\right.\)
TH2.\(\left\{{}\begin{matrix}1+3y=-11\\x+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-4\\x=1\end{matrix}\right.\)
Vậy,(x;y)=(-35;0),(1;-4)
HB
1
7 tháng 12 2015
3x -xy + 6y- 18 = 4 -18
x(3-y) + 6(y -3) = -14 => x(y-3) -6(y-3) =14
(y-3)(x-6) =14
| y-3 | 1 | -1 | 14 | -14 | 2 | -2 | 7 | -7 |
| x-6 | 14 | -14 | 1 | -1 | 7 | -7 | 2 | -2 |
| y | 4 | 2 | 17 | -11 | 5 | 1 | 10 | -4 |
| x | 20 | -8 | 7 | 5 | 13 | -1 | 8 | 4 |
HB
0
14 tháng 1 2023
Sửa đề: Tìm cặp \(x,y\in Z\) thỏa mãn \(x^2+3xy+2y^2+3x+6y-4=0\).
\(x^2+3xy+2y^2+3x+6y-4=0\)
\(\Leftrightarrow x^2+2xy+xy+2y^2+3x+6y=4\)
\(\Leftrightarrow\left(x^2+2xy\right)+\left(xy+2y^2\right)+\left(3x+6y\right)=4\)
\(\Leftrightarrow x\left(x+2y\right)+y\left(x+2y\right)+3\left(x+2y\right)=4\)
\(\Leftrightarrow\left(x+2y\right)\left(x+y+3\right)=4\)
Vì \(x,y\in Z\Rightarrow\left(x+2y\right)\left(x+y+3\right)\in Z\)
Trường hợp 1: \(\left\{{}\begin{matrix}x+2y=1\\x+y+3=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\) (thỏa mãn)
Trường hợp 2: \(\left\{{}\begin{matrix}x+2y=4\\x+y+3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-8\\y=6\end{matrix}\right.\) (thỏa mãn)
Trường hợp 3: \(\left\{{}\begin{matrix}x+2y=2\\x+y+3=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=3\end{matrix}\right.\) (thỏa mãn)
Trường hợp 4: \(\left\{{}\begin{matrix}x+2y=-2\\x+y+3=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-8\\y=3\end{matrix}\right.\) (thỏa mãn)
Vậy: \(\left(x,y\right)=\left[\left(1;0\right),\left(-8;6\right),\left(-4;3\right),\left(-8;3\right)\right]\)
11 tháng 9 2018
Đề bài yêu cầu gì ?? Phân tích đa thức thành nhân tử hay tính ?
27 tháng 11 2021
x2 - 3xy + 2x - 6y
= x (x + 2) - 3y (x + 2)
= (x+2) (x - 3y)
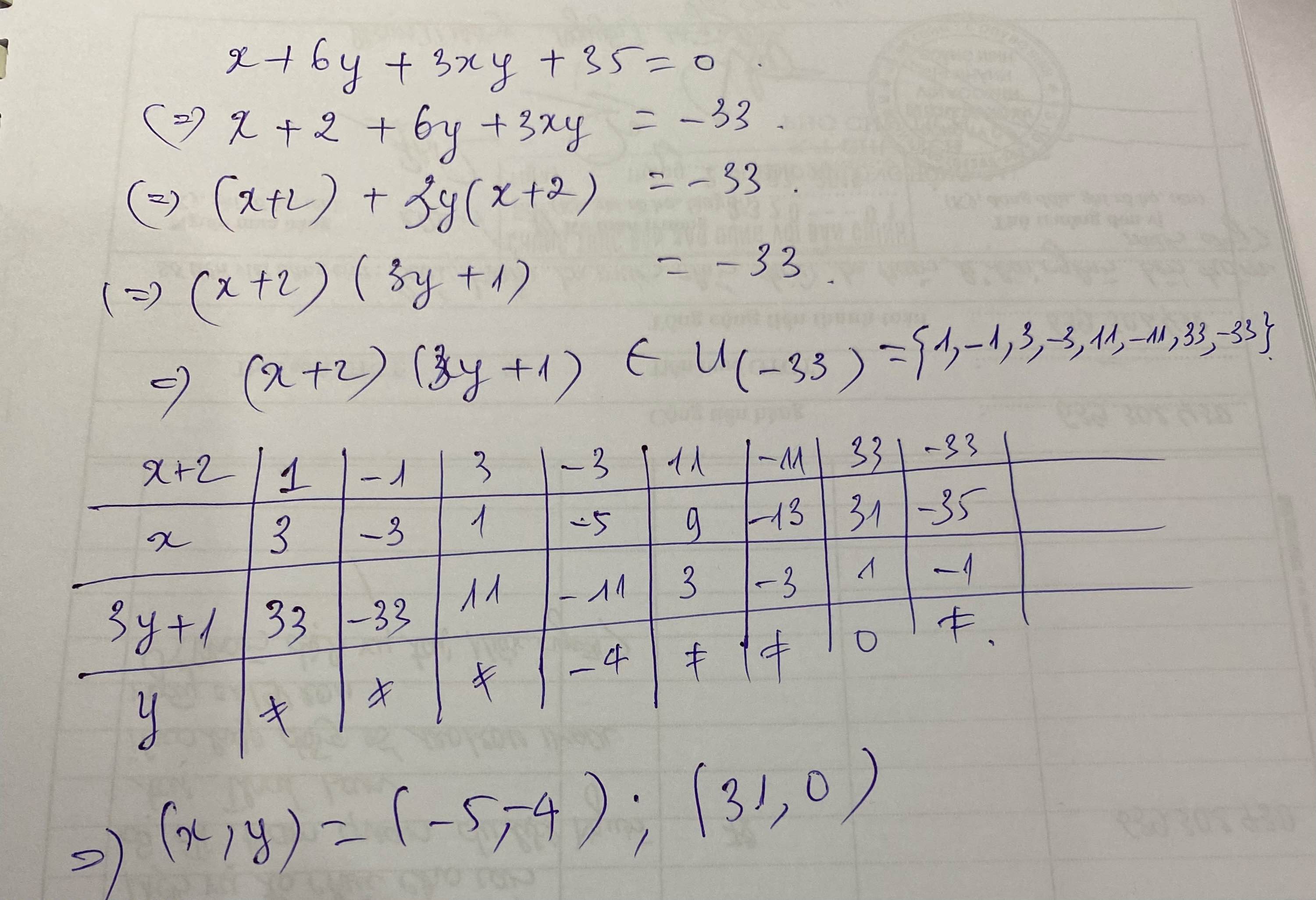
*Bổ sung đề: `x,y` nguyên
Ta có:
`3xy-x+6y=17`
`=>x(3y-1)+(6y-2)=15`
`=>x(3y-1)+2(3y-1)=15`
`=>(x+2)(3y-1)=15`
Ta có bảng sau:
Mà `x,y` nguyên => `(x;y)={(-17;0);(1;2)}`
3xy - x + 6y = 17
=> x(3y-1) +6y =17
=> x(3y - 1) + (6y -2) = 15
=> (x+2)(3y -1)=15
vì 3y chia hết cho 3
=> 3y-1 ko chia hết cho 3
=>3y-1 ko thuộc 3,-3,15,-15
ta có bảng sau :
=>(x,y) thuộc (-17,0);(1,2)
Vậy (x,y) thuộc (-17,0);(1,2)