Tìm x,y,z biết: \(\dfrac{x}{2}\)=\(\dfrac{y}{3}\)=\(\dfrac{z}{5}\) và xyz = 810
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DQ
4
QQ
2
1 tháng 3 2022
c: \(\Leftrightarrow x\left(x+3\right)=3+x-3\)
\(\Leftrightarrow x^2+3x-x=0\)
=>x(x+2)=0
=>x=0(loại) hoặc x=-2(nhận)
d: \(\Leftrightarrow\left(x+2\right)\left(x+3\right)+\left(x-2\right)\left(x-3\right)=2x^2+12\)
\(\Leftrightarrow2x^2+12=2x^2+12\)
=>0x=0(luôn đúng)
e: \(\Leftrightarrow x\left(x-3\right)+3\left(x-2\right)=3x-20\)
\(\Leftrightarrow x^2-6-3x+20=0\)
\(\Leftrightarrow x^2-3x+14=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot14=9-56< 0\)
Do đó: Phương trình vô nghiệm
1 tháng 3 2022
Gợi ý:
ĐKXĐ : Mẫu ≠ 0, từ đó bạn tự xác định
c) Tách \(^{^2x}\)- 3 thành x (x-3) -> quy đồng mẫu-> rút gọn -> tự làm
d) Tách \(^{^2x}\)-9 thành hằng đẳng thức -> như trên
e) Tách \(^{^2x}\)- 5 thành hằng đẳng thức -> như trên
f) Quy đồng mẫu, quá dễ nên không nói thêm
g) Tách \(^{^2x}\)- 1 thành hằng đẳng thức -> như trên
10 tháng 3 2022
a, bạn tự giải
b, \(\Delta=\left(m+1\right)^2-4m=\left(m-1\right)^2\ge0\)
Vậy pt luôn có 2 nghiệm x1 ; x2
c, Thay x = 1 ta được \(1+m+1+m=0\Leftrightarrow2m+2=0\Leftrightarrow m=-1\)
Thay m = -1 vào ta được \(x^2-1=0\Leftrightarrow x=1;x=-1\)
hay nghiệm còn lại là -1
NM
2
TV
2
Y
29 tháng 4 2023
Điều kiện xác định :
\(\left\{{}\begin{matrix}2x-2\ne0\\x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne2\\x\ne1\end{matrix}\right.\)
\(\Leftrightarrow x\ne1\)
\(\dfrac{2x+1}{2x-2}=\dfrac{2}{x-1}\)
\(\Leftrightarrow\dfrac{2x+1}{2x-2}-\dfrac{2}{x-1}=0\)
\(\Leftrightarrow\dfrac{2x+1}{2\left(x-1\right)}-\dfrac{2}{x-1}=0\)
\(\Leftrightarrow\dfrac{2x+1-2.2}{2\left(x-1\right)}=0\)
\(\Leftrightarrow2x+1-4=0\)
\(\Leftrightarrow2x-3=0\)
\(\Leftrightarrow x=\dfrac{3}{2}\left(tmdk\right)\)
Vậy \(S=\left\{\dfrac{3}{2}\right\}\)
LA
29 tháng 3 2022
a) 2x2 - 6x -1 = 0
delta phẩy = 9 + 2 = 11 = (\(\sqrt{11}\))2
x1 = \(\dfrac{3+\sqrt{11}}{2}\)
x2 = \(\dfrac{3-\sqrt{11}}{2}\)
b) xét delta phẩy có :
9 - 2.(2m-5) = 19 - 4m
+) điều kiện để phương trình vô nghiệm là 19 - 4m < 0 => m > \(\dfrac{19}{4}\)
+) điều kiện để phương trình có nghiệm kép là 19 - 4m = 0 => m = \(\dfrac{19}{4}\)
+) điều kiện để phương trình có 2 nghiệm phân biệt là 19 - 4m > 0
=> m < \(\dfrac{19}{4}\)
CM
23 tháng 12 2017
a, x 2 − 2 ( m + 1 ) x + m 2 + m − 1 = 0 (1)
Với m = 0, phương trình (1) trở thành:
x 2 − 2 x − 1 = 0 Δ ' = 2 ; x 1 , 2 = 1 ± 2
Vậy với m = 2 thì nghiệm của phương trình (1) là x 1 , 2 = 1 ± 2
b) Δ ' = m + 2
Phương trình (1) có hai nghiệm phân biệt ⇔ m > − 2
Áp dụng hệ thức Vi-ét, ta có: x 1 + x 2 = 2 ( m + 1 ) x 1 x 2 = m 2 + m − 1
Do đó:
1 x 1 + 1 x 2 = 4 ⇔ x 1 + x 2 x 1 x 2 = 4 ⇔ 2 ( m + 1 ) m 2 + m − 1 = 4 ⇔ m 2 + m − 1 ≠ 0 m + 1 = 2 ( m 2 + m − 1 ) ⇔ m 2 + m − 1 ≠ 0 2 m 2 + m − 3 = 0 ⇔ m = 1 m = − 3 2
Kết hợp với điều kiện ⇒ m ∈ 1 ; − 3 2 là các giá trị cần tìm.
13 tháng 3 2021
a) Thay m=-2 vào pt:
\(x^2-2.\left(-2+1\right).x-\left(-2+2\right)=0\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow x.\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Với m= -2 => S= {-2;0}
b) Để phương trình trên có 1 nghiệm x1=2:
<=> 22 -2.(m+1).2-(m+2)=0
<=> 4-4m -4 -m-2=0
<=> -5m=2
<=>m=-2/5
c) ĐK của m để pt trên có nghiệm kép:
\(\Delta'=0\\ \Leftrightarrow\left(m+1\right)^2+1.\left(m+2\right)=0\\ \Leftrightarrow m^2+3m+3=0\)
Vô nghiệm.
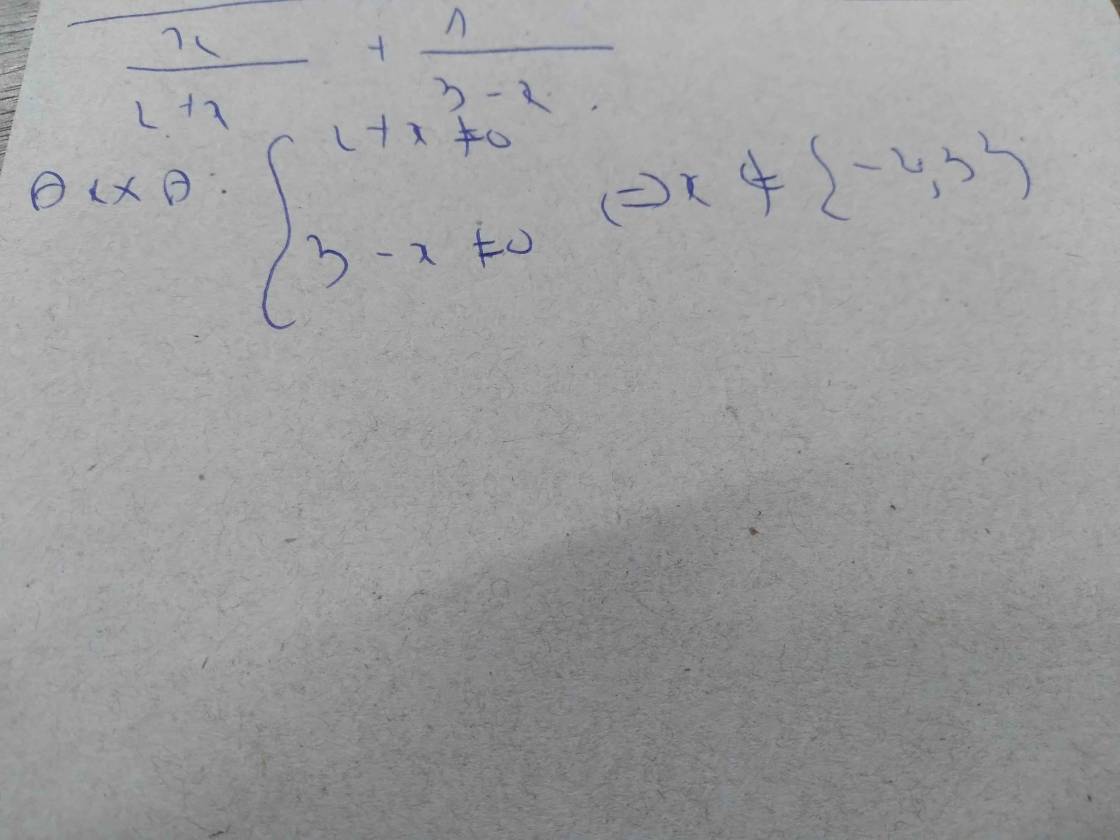
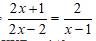
Giải:
\(\dfrac{x}{2}\) = \(\dfrac{y}{3}\) = \(\dfrac{z}{5}\) ⇒ (\(\dfrac{x}{2}\))3 = \(\dfrac{x}{2}.\dfrac{y}{3}.\dfrac{z}{5}\) = \(\dfrac{810}{30}\) = 27
⇒ (\(\dfrac{x}{2}\))3 = (3)3 ⇒ \(\dfrac{x}{2}\) = 3 ⇒ \(x\) = 3.2 ⇒ \(x=6\)
⇒ \(\dfrac{x}{2}\) = \(\dfrac{y}{3}\) = \(\dfrac{z}{5}\) = \(\dfrac{6}{2}\) = 3 ⇒ y = 3.3 = 9; z = 3.5 = 15
Vậy(\(x;y;z\)) = (6; 9; 15)