Tìm x biết:
x.(x-5).(x+12)=0
S.O.S nhanh nha rồi tick choa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BH
1
Những câu hỏi liên quan
7 tháng 2 2019
Bài 1 :
Mình nghĩ phải sửa đề ntn :
\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)\right]^2-\left[3\left(x+3\right)\right]^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)-3\left(x+3\right)\right]\left[2\left(2x+7\right)+3\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(4x+14-3x-9\right)\left(4x+14+3x+9\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(7x+23\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\7x+23=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{-23}{7}\end{cases}}}\)
Vậy....
b) \(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt \(q=x^2+x+1\)ta có :
\(A=q\left(q+1\right)-12\)
\(A=q^2+q-12\)
\(A=q^2+4q-3q-12\)
\(A=q\left(q+4\right)-3\left(q+4\right)\)
\(A=\left(q+4\right)\left(q-3\right)\)
Thay \(q=x^2+x+1\)ta có :
\(A=\left(x^2+x+1+4\right)\left(x^2+x+1-3\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+x-2\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+2x-x-2\right)\)
\(A=\left(x^2+x+5\right)\left[x\left(x+2\right)-\left(x+2\right)\right]\)
\(A=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
1 tháng 11 2021
a: \(=9-4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=9-4=5\)
b: \(=\sqrt{5}-2-\dfrac{1}{2}\cdot2\sqrt{5}=-2\)
2 tháng 11 2021
Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)
1 tháng 11 2021
\(1,\\ a,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ b,=a^2\left(a-x\right)-y\left(a-x\right)=\left(a^2-y\right)\left(a-x\right)\\ c,=\left(x-y\right)^2-z\left(x-y\right)=\left(x-y\right)\left(x-y-z\right)\\ d,=x\left(x-2y\right)+t\left(x-2y\right)=\left(x+t\right)\left(x-2y\right)\\ 2,\\ \Rightarrow x^2-4x+4-x^2+9=6\\ \Rightarrow-4x=-7\Rightarrow x=\dfrac{7}{4}\\ 3,\\ a,x^2+2x+2=\left(x+1\right)^2+1\ge1>0\\ b,-x^2+4x-5=-\left(x-2\right)^2-1\le-1< 0\)
CM
29 tháng 11 2018
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
CM
4 tháng 6 2017
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: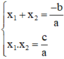 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
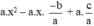
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm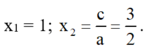 
Vậy: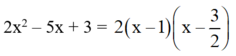 
25 tháng 10 2016
x4 - 12x2 + 12x - 9 = (x4 - 3x3) + (3x3 - 9x2) + (- 3x2 + 9x) + (3x - 9)
= (x - 3)(x3 + 3x2 - 3x + 3) = 0
2 tháng 11 2016
a) x4-12x3+12x-9=(x4-3x3)+(3x3-9x2)-(3x2-9x)+(3x-9)=x3(x-3)+3x2(x-3)-3x(x-3)+3(x-3)
=(x-3)(x3+3x2-3x+3)
b)P(x)=o=>x-3=0 và x3=3x2-3x+3=0
=>x=3 và x=rỗng
=>x=3
CM
30 tháng 8 2017
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
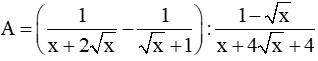
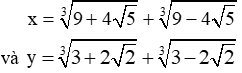
\(x.\left(x-5\right)\).(\(x+12\)) = 0
\(\left[{}\begin{matrix}x=0\\x-5=0\\x+12=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=5\\x=-12\end{matrix}\right.\)
Vậy \(x\in\) {-12; 0; 5}