Giải hệ phương trình
x3+y3=1
x2y+2xy2+y3=2
Cảm ơn các bạn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 9 2019
Cách 1
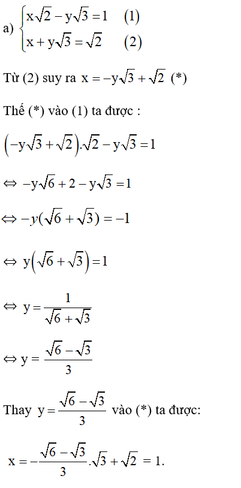
Vậy hệ phương trình có nghiệm duy nhất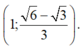 
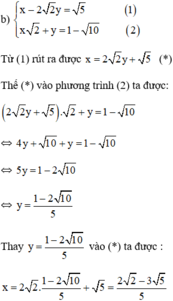
Vậy hệ phương trình có nghiệm duy nhất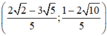 
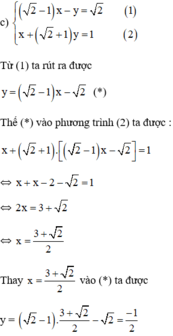
Vậy hệ phương trình có nghiệm duy nhất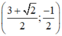 
Cách 2
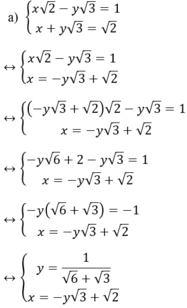
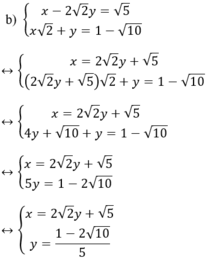
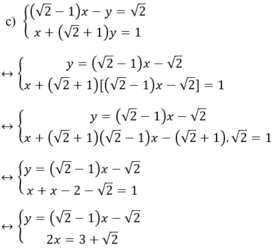
Kiến thức áp dụng
Giải hệ phương trình ta làm như sau:
Bước 1: Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
CM
23 tháng 11 2017
x 2 - y 3 = 1 1 5 x - 8 y = 3 2
Từ (1) ta rút ra được :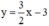 
(*)
Thế (*) vào phương trình (2) ta được :
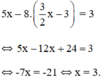
Thay x = 3 vào (*) ta suy ra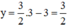 
Vậy hệ phương trình có nghiệm duy nhất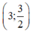 
CM
25 tháng 6 2018
Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.
Cách 1:
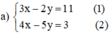
Từ (1) ta rút ra được y = 3 2 x − 11 2 (*)
Thế (*) vào phương trình (2) ta được :
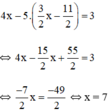
Thay x = 7 vào (*) ta suy ra y = 3 2 ⋅ 7 − 11 2 = 5
Vậy hệ phương trình có nghiệm duy nhất (7 ; 5).
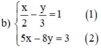
Từ (1) ta rút ra được : y = 3 2 x − 3 (*)
Thế (*) vào phương trình (2) ta được :
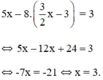
Thay x = 3 vào (*) ta suy ra
Vậy hệ phương trình có nghiệm duy nhất (3; 3/2)
Cách 2:
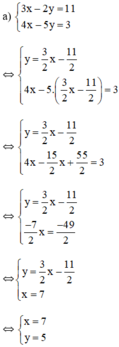
Vậy hệ phương trình có nghiệm duy nhất (7; 5).
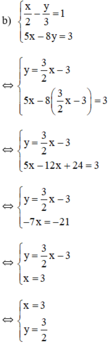
Vậy hệ phương trình có nghiệm duy nhất (3; 3/2)
Kiến thức áp dụng
Giải hệ phương trình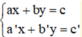 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
PB
1
14 tháng 11 2021
\(VT=\dfrac{2x^2+2xy+xy+y^2}{x^2\left(2x+y\right)-y^2\left(2x+y\right)}=\dfrac{2x\left(x+y\right)+y\left(x+y\right)}{\left(x^2-y^2\right)\left(2x+y\right)}\\ =\dfrac{\left(2x+y\right)\left(x+y\right)}{\left(2x+y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}=VP\)
CM
16 tháng 10 2019
x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 ) ( 1 )
– Xét x = 0, hệ (I) trở thành 4 y = y 3 y 2 = 4 < = > y = ± 2
– Xét x ≠ 0, đặt y x = t < = > y = x t . Hệ (I) trở thành
x 3 + 4 x t = x 3 t 3 + 16 x 1 + x 2 t 2 = 5 ( 1 + x 2 ) < = > x 3 ( t 3 − 1 ) = 4 x t − 16 x x 2 ( t 2 − 5 ) = 4 < = > x 3 ( t 3 − 1 ) = 4 x ( t − 4 ) ( 1 ) 4 = x 2 ( t 2 − 5 ) ( 2 )
Nhân từng vế của (1) và (2), ta được phương trình hệ quả
4 x 3 ( t 3 − 1 ) = 4 x 3 ( t − 4 ) ( t 2 − 5 ) < = > t 3 − 1 = t 3 − 4 t 2 − 5 t + 20 (Do x ≠ 0) <=>4t 2 + 5 t − 21 = 0 < = > t = − 3 t = 7 4
+ Với t = – 3, thay vào (2) được x2 = 1 ⇔ x = ±1.
x = 1 thì y = –3, thử lại (1;–3) là một nghiệm của (I)
x = –1 thì y = 3, thử lại (–1;3) là một nghiệm của (I)
+ Với t = 7/4 , thay vào (2) được x 2 = − 64 31 (loại)
Vậy hệ (I) có các nghiệm (0;2), (0;–2), (1;–3), (–1;3).
CM
23 tháng 1 2017
Ta có
x 2 − y 3 = 1 x + y 3 = 2 ⇔ x 2 − y 3 = 1 x 2 + y 6 = 2 ⇔ x 2 − y 3 = 1 6 + 3 y = 1 ⇔ x 2 − y 3 = 1 y = 1 6 + 3 ⇔ y = 6 − 3 3 x 2 − 3 . 6 − 3 3 = 1 ⇔ y = 6 − 3 3 x = 1
Vậy hệ đã cho có nghiệm duy nhất ( x ; y ) = 1 ; 6 − 3 3
Đáp án: D