Cho 3 số nguyên a, b và c thoả mãn a + b + c + abc chia hết cho 3. Chứng minh (a + b)(b + c)(c + a) chia hết cho 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
MH
22 tháng 9 2023
\(a^3+b^3+c^3=\left(a+b+c\right)^3-3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Ta có: Với 3 số a,b,c ít nhất có 1 cặp a,b,c cùng chẵn hoặc cùng lẻ
=> \(\left[{}\begin{matrix}a+b⋮2\\b+c⋮2\\c+a⋮2\end{matrix}\right.\)=> \(3\left(a+b\right)\left(b+c\right)\left(c+a\right)⋮6\)
=> \(a^3+b^3+c^3⋮6\)
2 tháng 7 2023
a: a^3-a=a(a^2-1)
=a(a-1)(a+1)
Vì a;a-1;a+1 là ba số liên tiếp
nên a(a-1)(a+1) chia hết cho 3!=6
=>a^3-a chia hết cho 6
0
Cho P=(a+b)(b+c)(a+c)+abc
Nếu a,b,c thuộc Z và a+b+c chia hết cho 6
Chứng minh P-3abc chia hết cho 6
1
12 tháng 12 2017
P - 3abc = (a+b)(b+c)(a+c)+abc - 3abc
= (a+b+c-c)(b+c)(a+c) - 2abc
= (a+b+c)(b+c)(a+c) - c(b+c)(a+c) - 2abc
= (a+b+c)(b+c)(c+a) - c(ab + bc +ac +c2) - 2abc
= (a+b+c)(b+c)(a+c) - c( ab +bc + ac +c2+ 2ab)
= (a+b+c)(b+c)(c+a) - c[(bc+c2+ac) + 3ab]
= (a+b+c)(b+c)(c+a) - c[c(b+c+a) + 3ab]
= (a+b+c)(b+c)(c+a) - c²(a+b+c) - 3abc
Ta có: a + b + c chia hết cho 6
⇒mà 6 ⋮ 2
⇒ a+b+c chia hết cho 2
⇒ a+b+c là số chẵn
⇒ trong 3 số a, b, c phải có ít nhất một số chẳn
⇒ abc ⋮ 2
⇒ 3abc ⋮ 6
mà a+b+c chia hết cho 6
⇒ (a+b+c)(b+c)(c+a) chia hết cho 6
c²(a+b+c) chia hết cho 6
⇒ (a+b+c)(b+c)(c+a) - c²(a+b+c) - 3abc chia hết cho 6
Vậy P - 3abc chia hết cho 6.
OK
0
12 tháng 12 2021
Bài 1:
\(a,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\\ A=\left(1+2\right)\left(2+2^3+...+2^{2009}\right)=3\left(2+...+2^{2009}\right)⋮3\\ A=\left(2+2^2+2^3\right)+...+\left(2^{2008}+2^{2009}+2^{2010}\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{2008}\right)=7\left(2+...+2^{2008}\right)⋮7\)
\(b,\left(\text{sửa lại đề}\right)B=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\\ B=\left(1+3\right)\left(3+3^3+...+3^{2009}\right)=4\left(3+3^3+...+3^{2009}\right)⋮4\\ B=\left(3+3^2+3^3\right)+...+\left(3^{2008}+3^{2009}+3^{2010}\right)\\ B=\left(1+3+3^2\right)\left(3+...+3^{2008}\right)=13\left(3+...+3^{2008}\right)⋮13\)
12 tháng 12 2021
Bài 2:
\(a,\Rightarrow2A=2+2^2+...+2^{2012}\\ \Rightarrow2A-A=2+2^2+...+2^{2012}-1-2-2^2-...-2^{2011}\\ \Rightarrow A=2^{2012}-1>2^{2011}-1=B\\ b,A=\left(2020-1\right)\left(2020+1\right)=2020^2-2020+2020-1=2020^2-1< B\)
24 tháng 11 2019
+ Theo bài, ta có: a+b+c chia hết cho 6
=> a+b+c=6
+ M=(a+b)(b+c)(c+a)-2abc
M=(6-c)(6-a)(6-b)-2abc
M=(12-6a-6c+ac)(6-b)-2abc
M=72-12b-12a+6ab-12c+6cb+6ac-abc-2abc
M=72-12(a+b+c)+6(ab+cb+ac)-3abc
+ có:72 chia hết cho 6
12 chia hết cho 6
6 chia hết cho 6
=> M chia hết cho 6
Vậy...
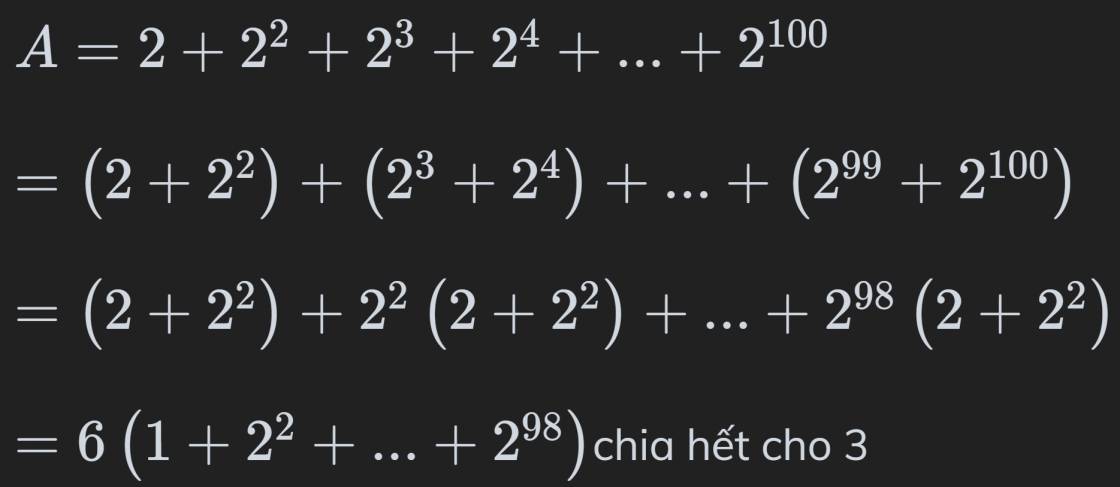
Đặt \(P=\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Trước tiên ta sẽ chứng minh \(P\) chẵn.
Ta thấy rằng một số nguyên thì hoặc là số chẵn, hoặc là số lẻ. Tuy nhiên, ta có tới 3 số nguyên a, b, c. Điều này có nghĩa là sẽ tồn tại ít nhất 2 số trong 3 số a, b, c có cùng tính chẵn lẻ (nguyên lý Dirichlet). Khi đó tổng của 2 số này là một số chẵn \(\Rightarrow\) P chẵn.
Ta chứng minh \(P⋮3\)
Nếu trong 3 số a, b, c có ít nhất một số chia hết cho 3, không mất tính tổng quát, giả sử số đó là a. Khi đó vì \(a,abc,a+b+c+abc\) đều chia hết cho 3 nên \(b+c⋮3\) \(\Rightarrow P⋮3\)
Nếu trong 3 số a, b, c không có số nào chia hết cho 3 thì sẽ có 2 trường hợp:
TH1: Cả 3 số này khi chia cho 3 có cùng số dư.
Khi đó \(a+b+c⋮3\) trong khi \(abc⋮̸3\Rightarrow a+b+c+abc⋮̸3\), không thỏa mãn.
TH2: 3 số a, b, c chia cho 3 không có cùng số dư. Khi đó tồn tại một số chia 3 dư 1 và một số chia 3 dư 2. Tổng của 2 số này sẽ chia hết cho 3 \(\Rightarrow P⋮3\)
Vậy \(P⋮3\)
Ta có \(P⋮2,P⋮3\) và \(ƯCLN\left(2,3\right)=1\) nên \(P⋮6\). Ta có đpcm.
\(a\) \(\Rightarrow b+c⋮3\)