Tìm x biết 4 |2x+3|=12x + 28
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 1 2017
a, 128 – 3(x+4) = 23
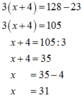
b, 12 x - 4 3 . 8 3 = 4 . 8 4
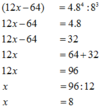
c, [(4x+28).3+55]:5 = 35
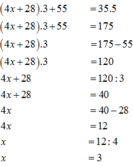
d, 720:[41 – (2x – 5)] = 2 3 . 5
21 tháng 3 2020
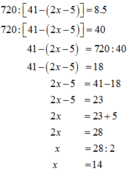
a,
128-3x-12=23
3x=128-12-23
3x=93
x=93:3
= 31
b,
(12x+84+55):5=35
12x+84+55=35.5
12x+84+55=175
12x=175-55-84
12x=36
x=36:12
x=3
NM
19 tháng 9 2023
\(a,128-3.\left(x+4\right)=23\\ \Rightarrow3.\left(x+4\right)=105\\ \Rightarrow x+4=35\\ \Rightarrow x=31\\ b,\left[\left(4x+28\right).3+55\right]:5=35\\ \Rightarrow\left(4x+28\right).3+55=175\\ \Rightarrow4x+28.3=120\\ \Rightarrow4x+28=60\\ \Rightarrow4x=32\\ \Rightarrow x=8.\)
KV
19 tháng 9 2023
c) \(\left(12x-4^3\right).8^3=4.8^4\)
\(12x-64=4.8^4:8^3\)
\(12x-64=32\)
\(12x=32+64\)
\(12x=96\)
\(x=\dfrac{96}{12}\)
\(x=8\)
d) \(720:\left[41-\left(2x-5\right)\right]:5=35\)
\(720:\left(41-2x+5\right):5=35\)
\(720:\left(46-2x\right)=35.5\)
\(720:\left(46-2x\right)=175\)
\(46-2x=720:175\)
\(46-2x=\dfrac{144}{35}\)
\(2x=46-\dfrac{144}{35}\)
\(2x=\dfrac{1466}{35}\)
\(x=\dfrac{1466}{35}:2\)
\(x=\dfrac{733}{35}\)
3 tháng 2 2022
a: =>3(x+4)=115
=>x+4=115/3
hay x=103/3
b: =>\(8^3\cdot\left(12x-64\right)=4\cdot8^4\)
\(\Leftrightarrow12x-64=32\)
=>12x=96
hay x=8
c: \(\Leftrightarrow\left(4x+28\right)\cdot23+55=175\)
=>(4x+28)x23=120
=>4x+28=120/23
=>4x=-524/23
hay x=-131/23
8 tháng 11 2017
128-3.(x+4) =23
3.(x+4) =128-23
3.(x+4) = 105
x+4 =105:3
x+4 =35
x = 35-4
x=31
13 tháng 8 2020
a)120-3(x+4)=23
=>3(x+4)=120-23
=>3(x+4)=97
=>x+4=97:3
=>x+4=\(\frac{97}{3}\)
=>x=\(\frac{97}{3}\)-4
=>x=\(\frac{85}{3}\)
Vậy x=\(\frac{85}{3}\)
b)[(4x+28).3+55]:5=35
=>(4x+28).3+55=35.5
=>(4x+28).3+55=175
=>(4x+28).3=175-55
=>(4x+28).3=120
=>4x+28=120:3
=>4x+28=40
=>4x=40-28
=>4x=12
=>x=12:4
=>x=3
Vậyx= 3
c)\((12x-4^3).8^3=4.8^4\)
=>\(12x-64=4.8^4:8^3\)
=>12x-64=4.8
=>12x-64=32
=>12x=96
=>x=96:12
=>x=8
Vậy x=8
d)720:[41-(2x-5)]=23.5
=>720:[41-2x-5)]=40
=>41-(2x-5)=720:40
=>41-(2x-5)=18
=>2x-5=41-18
=>2x-5=23
=>2x=23+5
=>2x=28
=>x=28:;2
=>x=14
Vậy x=14
VD
13 tháng 8 2020
a, 120 - 3 [ x+4]=23
3 [x+4]= 120-23 = 97
3x = 97-4
3x= 93
x= 93:3
x=31
em bt làm mỗi bài này thui mà ko bt đúng ko
BD
1
9 tháng 2 2017
a) 3x2 + 12x =0
<=> 3x( x+ 4)=0
<=> \(\orbr{\begin{cases}3x=0\\x+4=0\end{cases}}\) <=>\(\orbr{\begin{cases}x=0\\x=-4\end{cases}}\)
d) \(4x^3=4x\)
<=> \(4x^3-4x=0\)
<=> 4x( x2 -1) =0
<=> 4x ( x - 1) ( x+ 1) =0
<=> 4x=0 hoac x-1=0 hoac x+1=0
<=> x=0 hoac x=1 hoac x=-1