\(\dfrac{x+1}{3x+2}\)tiệm cận ngang là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\lim\limits_{x\rightarrow-\infty}\dfrac{1+\dfrac{1}{x}}{-\left(m^2+1\right)\sqrt[]{1-\dfrac{4}{x^2}}}=-\dfrac{1}{m^2+1}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{1}{m^2+1}\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận ngang
\(\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{3}{0}=\infty\)
\(\lim\limits_{x\rightarrow-2^-}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{-1}{0}=\infty\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy ĐTHS có 4 tiệm cận
4 tháng 9 2021
tại sao nơi chỗ lim\(_{x->2^+}\) và limx->-2- ở dưới mẫu lại bằng 0 vậy ạ?
AS
1
AH
Akai Haruma
Giáo viên
29 tháng 5 2021
Lời giải:
TXĐ: \((-\infty; -1)\cup (-1;+\infty)\)
\(\lim\limits_{x\to +\infty}y=\lim\limits_{x\to +\infty}\frac{1+\sqrt{1+\frac{1}{x}}}{1+\frac{1}{x}}=\frac{1+1}{1}=2\)
\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to -\infty}\frac{-1+\sqrt{1+\frac{1}{x^2}}}{-1+\frac{1}{-x}}=\frac{-1+1}{-1}=0\)
Do đó ĐTHS có 2 TCN là $y=0$ và $y=2$
\(\lim\limits_{x\to -1-}y=\lim\limits_{x\to -1-}\frac{x+\sqrt{x^2+1}}{x+1}=-\infty\) do \(\lim\limits_{x\to -1-}(x+\sqrt{x^2+1})=\sqrt{2}-1>0\) và \(\lim\limits_{x\to -1-}\frac{1}{x+1}=-\infty\)
Tương tự \(\lim\limits_{x\to -1+}y=+\infty\) nên $x=-1$ là TCĐ của đths
Vậy có tổng 3 TCN và TCĐ
11 tháng 1 2024
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-5-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
=>Đường thẳng \(y=\dfrac{m-5}{2}\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\)
Để đường tiệm cận ngang \(y=\dfrac{m-5}{2}\) đi qua M(-2;1) thì \(\dfrac{m-5}{2}=1\)
=>m-5=2
=>m=7
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
=>\(y=2m-1\) là đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
=>2m-1=1
=>2m=2
=>m=1
11 tháng 1 2024
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
\(\lim\limits_{x\rightarrow-1^+}\dfrac{2x-1}{x+1}=-\infty\Rightarrow x=-1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow+\infty}\dfrac{2x-1}{x+1}=2\Rightarrow y=2\) là tiệm cận ngang
\(\Rightarrow P=3.\left(-1\right)^2-2=1\)
HL
1
28 tháng 12 2017
bài cơ bản mà !
mẫu =0 có 2 nghiệm
x=2, x=-1 là 2 đường tc đứng
bật tử bé hơn bật mẫu => có tiệm cận ngang y=0
17 tháng 1 2018
sorry bạn nhé. bạn nhẩm nghiệm sai rồi :)
nghiệm là \(\dfrac{3\pm\sqrt{17}}{2}\) bạn nhé. và nếu như mẫu có nghiệm là x= -1 thì bạn sẽ phải ;oại nghiệm này vì nó cũng là nghiệm của tử = 0 thì lim của nó sẽ k tiến đến vô cùng bạn nhé nên x=-1 k phải là tiệm cận đứng
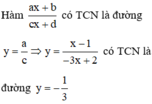
y=1/3