giúp mình câu b vs ạa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 12 2021
Bài 33:
a: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)
NT
1
12 tháng 1 2022
Câu 18: B
Câu 19: B
Câu 20: D
Câu 21; D
Câu 22: B
Câu 23: B
Câu 24: A
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
13 tháng 12 2023
\(a,D=\dfrac{m}{V}=\dfrac{3,9}{0,5}=7,8\left(\dfrac{kg}{dm^3}\right)=7800\left(\dfrac{kg}{m^3}\right)=7,8\left(\dfrac{g}{cm^3}\right)\)
b, Vậy khối kim loại trên là một khối sắt
c, \(d=10D=10.7800=78000\left(\dfrac{N}{m^3}\right)\)
Q
1
16 tháng 10 2023
Ư(240)={1;2;3;4;5;6;8;10;12;15;16;20;24;30;40;48;60;80;120;240}
Trong các số này thì các số là bội của 24 là:
24;48;120;240
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2022
\(A=3+3^2+...+3^{2005}\)
\(\Rightarrow3A=3^2+3^3+...+3^{2006}\)
\(\Rightarrow3A-A=3^{2006}-3\)
\(\Rightarrow2A=3^{2006}-3\)
\(\Rightarrow2A+3=3^{2006}\) là 1 lũy thừa của 3 (đpcm)
4.
\(B=1+1+2+2^2+2^3+...+2^{100}\)
\(2B=2+2+2^2+...+2^{101}\)
\(\Rightarrow2B-B=2+2^{101}-\left(1+1\right)=2^{101}\)
\(\Rightarrow B=2^{101}\) là 1 lũy thừa của 2 (đpcm)
8 tháng 12 2023
Bài 1:
\(A=2+2^2+2^3+...+2^{2003}+2^{2004}\)
\(=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{2002}+2^{2003}+2^{2004}\right)\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2002}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+2^4+...+2^{2002}\right)⋮7\)
Bài 2:
\(A=2+2^2+2^3+2^4+...+2^{59}+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\cdot\left(2+2^5+...+2^{57}\right)⋮15\)
Bài 3:
\(A=1+3+3^2+3^3+...+3^{1990}+3^{1991}\)
\(=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+...+\left(3^{1989}+3^{1990}+3^{1991}\right)\)
\(=13+3^3\left(1+3+3^2\right)+...+3^{1989}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{1989}\right)⋮13\)
Bài 4:
\(A=4+4^2+4^3+4^4+...+4^{23}+4^{24}\)
\(=\left(4+4^2\right)+\left(4^3+4^4\right)+...+\left(4^{23}+4^{24}\right)\)
\(=\left(4+4^2\right)+4^2\left(4+4^2\right)+...+4^{22}\left(4+4^2\right)\)
\(=20\left(1+4^2+...+4^{22}\right)⋮20\)
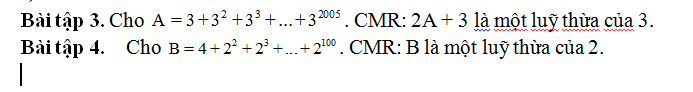
khai triển P, ta được:
\(P=\dfrac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{2xy^2+2yz^2+2zx^2+3xyz}\)
\(P=\dfrac{xy^2+yz^2+zx^2+x^2y+y^2z+z^2x+3xyz}{2xy^2+2yz^2+2zx^2+3xyz}-1\)
\(P=\dfrac{\left(x+y+z\right)\left(xy+yz+zx\right)}{2xy^2+2yz^2+2zx^2+3xyz}-1\)\(P=\dfrac{0}{2xy^2+2yz^2+2zx^2+3xyz}-1=-1\)