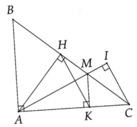
cho tam giác ABC có góc A là góc tù kẻ AH vuông góc với BC tại H . Gọi I là hình chiếu của B xuống AC , K là hình chiếu của C xuống AB. Chứng minh rằng AH, BI,CK đồng quy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAIH vuông tại H và ΔAKH vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAIH=ΔAKH
Suy ra: AI=AK
c: Ta có: AI=AK
nên A nằm trên đường trung trực của IK(1)
ta có: MI=MK
nên M nằm trên đường trung trực của IK(2)
ta có: HI=HK
nên H nằm trên đường trung trực của IK(3)
Từ (1), (2) và (3)suy ra A,M,H thẳng hàng

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAIH vuông tại H và ΔAKH vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAIH=ΔAKH
Suy ra: AI=AK
c: Ta có: AI=AK
nên A nằm trên đường trung trực của IK(1)
ta có: MI=MK
nên M nằm trên đường trung trực của IK(2)
ta có: HI=HK
nên H nằm trên đường trung trực của IK(3)
Từ (1), (2) và (3)suy ra A,M,H thẳng hàng

Bạn tự vẽ hình. Gợi ý:
- Chứng minh tứ giác AEHF là hình chữ nhật.
*Gọi K là giao điểm của AH và EF. Khi đó K là trung điểm AH.
- Chứng minh tam giác AHM cân tại A. Suy ra \(\widehat{MAB}=\widehat{HAB}\)
Mặt khác \(\widehat{HAB}=\widehat{ABI}\) (BI//AH) \(\Rightarrow\widehat{MAB}=\widehat{ABI}\)
\(\Rightarrow\)△ABI cân tại I nên AI=BI.
*CA cắt BI tại S. Chứng minh I là trung điểm BS.
Đến đây bài toán đã trở nên đơn giản hơn (chỉ chú ý vào các điểm C,A,H,B,S và K).
- CK cắt BS tại I'. Khi đó ta cũng c/m được I' là trung điểm BS.
\(\Rightarrow I\equiv I'\) nên C,K,I thẳng hàng.
Suy ra đpcm.

a/
\(AH^2=HB.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH=\sqrt{HB.HC}=\sqrt{4.9}=6cm\)
\(\tan\widehat{ABC}=\dfrac{AH}{HB}=\dfrac{6}{4}=\dfrac{3}{2}\)
b/
Xét tg vuông AHB có
\(HB^2=BD.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Xét tg vuông AHC có
\(HC^2=CE.AC\) (lý do như trên)
\(CE.BD.AC.AB=HB^2.HC^2=\left(HB.HC\right)^2\)
Mà \(HB.HC=AH^2\) (cmt)
\(\Rightarrow CE.BD.AC.AB=AH^4\)
c/
\(HD\perp AB;AC\perp AB\) => HD//AC => HD//AE
\(HE\perp AC;AB\perp AC\) => HE//AB => HE//AD
=> ADHE là hình bình hành mà \(\widehat{A}=90^o\) => ADHE là HCN
Xét tg vuông ADH và tg vuông ADE có
HD = AE (cạnh đối HCN)
AD chung
=> tg ADH = tg ADE (Hai tg vuông có 2 cạnh góc vuông = nhau)
\(\Rightarrow\widehat{AED}=\widehat{AHD}\)
\(\widehat{AHD}=\widehat{B}\) (cùng phụ với \(\widehat{BAH}\) )
\(\Rightarrow\widehat{AED}=\widehat{B}\) (1)
\(\widehat{C}+\widehat{B}=90^o\) (2)
\(\widehat{IAE}+\widehat{AED}=90^o\Rightarrow\widehat{IAE}+\widehat{B}=90^o\) (3)
Từ (2) và (3) => \(\widehat{IAE}=\widehat{C}\) => tg AIC cân tại I => IA=IC
Ta có
\(\widehat{IAE}+\widehat{BAI}=\widehat{A}=90^o\)
\(\Rightarrow\widehat{C}+\widehat{BAI}=90^o\) mà \(\widehat{C}+\widehat{B}=90^o\)
\(\Rightarrow\widehat{BAI}=\widehat{B}\) => tg ABI cân tại I => IA=IB
Mà IA= IC (cmt)
=> IB=IC => I là trung điểm của BC

a: BC vuông góc SA
BC vuôg góc AB
=>BC vuông góc (SAB)
b: BI vuông góc SA
BI vuông góc AC
=>BI vuông góc (SAC)