Cho tam giác $ABC$ có hai đường cao $B{B}'$ và $C{C}'$. Gọi $O$ là trung điểm của $BC$. Chứng minh đường tròn tâm $O$ bán kính $O{B}'$ đi qua $B$, $C$, ${C}'$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: Đường chéo AE,BD
Xét ΔAEC vuông tại E và ΔBDC vuông tại D có
góc C chung
Do đó: ΔAEC\(\sim\)ΔBDC
=>AC/BC=AE/BD=CE/CD
hay AC/CE=BC/CD
Xét ΔABC và ΔCED có
AC/CD=BC/CD
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔCED

a. Hình vẽ ( 1 điểm)
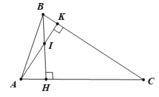
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)
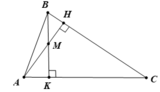
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)
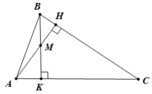
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)

Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)
/
ΔBC'C vuông tại C'
=>C' nằm trên đường tròn đường kính BC
=>OC'=OB=OC(2)
ΔB'BC vuông tại B'
=>B' nằm trên đường tròn đường kính BC
=>OB'=OB=OC(1)
Từ (1),(2) suy ra OC'=OB=OC=OB'
hay (O;OB') đi qua B,C,C'