Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{MBA}=90^0-55^0=35^0\)
\(\widehat{MAB}=90^0-67^0=23^0\)
Do đó: \(\widehat{AMB}=122^0\)

a. Hình vẽ ( 1 điểm)
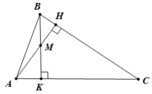
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)

Bài 2: Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Dang Khanh Ngoc - Toán lớp 7 - Học toán với OnlineMath

Ngày mai mình nộp bài rồi, mong các bạn chỉ bài giúp mình . mình không hiểu gì về 2 bài toán này cả TT_TT

Bạn tự vẽ hình nha
1. Xét tam giác EBH có: BE=BH (gt) -> tan giác EBH cân tại B -> góc BEH = góc BHE
Ta lại có góc ABH = góc BEH + góc BHE (góc ngoài của tam giác EBH); Mà góc BEH = góc BHE (cmt) -> góc ABH = 2 góc BEH; Mà góc ABH = 2 góc ACB (gt)-> góc BEH = góc ACB ( đpcm)
2. Ta có: góc BHE = góc DHC (2 góc đối đỉnh); Mà góc BHE = góc BEH (cmt) và góc BEH = góc ACB (cmt) => góc DHC = góc ACB -> tam giác DHC cân tại D -> DH = DC ( 2 cạnh tương ứng)
Ta có: tam giác AHC vuông tại H -> góc HAC +góc ACB = 90 độ (2 góc ở đáy tam giác vuông ); Mà góc AHD + góc DHC = 90 độ và góc ACB = góc DHC (cmt) -> góc HAC = góc AHD -> tam giác AHD cân tại D => DA = DH (2 cạnh tương ứng )
Vậy DH=DC=DA
3. Ta có tam giác ABB' có: BH = B'H ( H là trung điểm BB') -> AH là đường trung tuyến lại vừa là đường cao -> tam giác ABB' cân tại A -> góc ABH = góc AB'H (2 góc ở đáy)
Xét tam giác AB'C có: góc AB'H = góc B'AC + góc ACB' (góc ngoài); Mà góc ABH = góc AB'H (cmt) -> góc ABH = góc B'AC + góc ACB ; Mà góc ABH = 2 góc ACB'
-> góc B'AC = góc ACB' => tam giác AB'C cân tại B'
4. Bạn vẽ lại hình nha: giả sử tam giác ABC vuông tại A
Xét tam giác ADE và tam giác ABC có: góc A chung và góc BEH = góc ACB (cmt) -> hai tam giác đồng dạng theo trường hợp (g.g) -> góc ADE = góc ABC (2 góc tương ứng) (1)
Ta có : góc HAD = 90 độ - góc C ( tam giác HAC vuông tại H); Mà góc ABC = 90 độ - góc C ( tam giác ABC vuông tại A) -> góc HAD = góc ABC (2)
Từ (1) và (2) -> góc ADE = góc HAD; Mà góc HAD = góc AHD nên suy ra tam giác AHD đều
Xét tam giác ADE và tâm giác HAC có: góc EAD = góc CHA = 90 độ (gt); góc ADE = góc HAC (cmt); AD = AH (tam giác AHD đều) => tam giác ADE = tam giác HAC theo trường hợp (g.c.g)
=> DE = AC (2 cạnh tương ứng) => DE2 = AC2 ; Mà AC2 = BC2 - AB2 (định lí Py-ta-go trong tam giác ABC) => DE2 = BC2 - AB2 (đpcm)
Học tốt nhé 🙋♀️🙋♀️🙋♀️💗💗💗
a. Hình vẽ ( 1 điểm)
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)