a) chứng tỏ MN//PQ
b) tính số đo NQH
c)cho FME=35°,EPH=55°
Chứng tỏ ME vuông góc với EP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

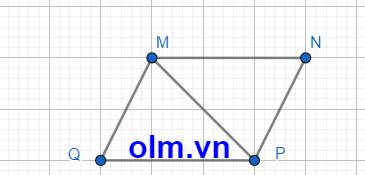
Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
\(\widehat{QPM}\) = \(\widehat{PMN}\) (2 góc so le trong)
\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)
\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)
\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)
b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
MN = PQ
\(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)
⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)
\(\Rightarrow\) MQ = NP (đpcm)
⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\)
Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:
QM // NP (đpcm)

bài 1 :
a) Ta có MQ//NP (theo giả thiết).
Chứng minh MN = PQ:
Vì MN//PQ và MQ//NP, ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
b) Ta có MN = PQ (theo giả thiết).
Chứng minh MQ//NP:
Giả sử MQ không // NP. Khi đó, MQ và NP sẽ cắt nhau tại một điểm O.
Vì MN//PQ và MQ//NP, nên ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Từ đó suy ra: MN/MQ = NP/NP
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Điều này mâu thuẫn với giả thiết MN = PQ (đã cho). Vậy giả sử MQ không // NP là sai.
Do đó, ta kết luận rằng MQ//NP.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
bài 2 :
a) Ta có MN = MQ và góc M = 50 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc N = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
50 độ + góc N + 90 độ + góc N = 360 độ
Simplifying the equation:
140 độ + 2góc N = 360 độ
Trừ 140 độ từ hai phía:
2góc N = 220 độ
Chia cho 2:
góc N = 110 độ
Vậy số đo góc MQN là 110 độ.
b) Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + 110 độ + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + 200 độ = 360 độ
Trừ 200 độ từ hai phía:
2góc M = 160 độ
Chia cho 2:
góc M = 80 độ
Vậy số đo góc MQP là 80 độ.
c) Để chứng minh MP vuông góc với NQ, ta cần chứng minh rằng góc MPN + góc NQP = 90 độ.
Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + góc N + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + góc N = 270 độ
Vì góc M = góc Q, nên ta có:
2góc M + góc M = 270 độ

Lời giải:
a) Xét tam giác $EDM$ và $EKQ$ có:
$\widehat{E}$ chung
$\widehat{EDM}=\widehat{EKQ}$ (hai góc đồng vị)
$\Rightarrow \triangle EDM\sim \triangle EKQ$ (g.g)
b)
$MD\parallel QK$ nên theo định lý Talet:
$\frac{EM}{EQ}=\frac{ED}{EK}\Rightarrow EM.EK=EQ.ED$

Sau khi đo ta có: MQ = NP = 3cm, MN = PQ = 4cm, ME = 1cm
Suy ra, NE = 4 - 1 = 3(cm)
Diện tích hình chữ nhật MNPQ là: 4 x 3 = 12 (c m 2 )
Diện tích tam giác MQE là: 3 x 1 2 = 1,5 (c m 2 )
Diện tích tam giác NEP là 3 × 3 2 = 4,5 (c m 2 )
Tổng diện tích 2 tam giác trên là: 1,5+4,5 = 6 (c m 2 )
Diện tích tam giác EQP là: 12 - 6 = 6(c m 2 )
Nói thêm: vì tổng diện tích hai tam giác MQE và NEP bằng diện tích tam giác EPQ (cùng bằng nửa diện tích hình chữ nhật MNPQ) nên ta cũng có thể tính tổng diện tích trên và diện tích tam giác EPQ như sau: 4 x 3 2 = 6 ( cm 2 )

Sau khi đo ta có: MQ = NP = 3cm, MN = PQ = 4cm, ME = 1cm
Suy ra, NE = 4 - 1 = 3(cm)
Diện tích hình chữ nhật MNPQ là:
4 x 3 = 12 (cm2)
Diện tích tam giác MQE là:
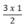 = 1,5 (cm2)
= 1,5 (cm2)
Diện tích tam giác NEP là:
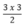 = 4,5 (cm2)
= 4,5 (cm2)
Tổng diện tích 2 tam giác trên là:
1,5 + 4,5 = 6 (cm2)
Diện tích tam giác EQP là:
12 - 6 = 6(cm2)
Nói thêm: vì tổng diện tích hai tam giác MQE và NEP bằng diện tích tam giác EPQ (cùng bằng nửa diện tích hình chữ nhật MNPQ) nên ta cũng có thể tính tổng diện tích trên và diện tích tam giác EPQ như sau:
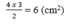
Hình đâu em?