cho tam giác abc vuông tại a đường cao ah từ m là một điểm bất kì trên cạnh bc kẻ md vuông góc với ab, me vuông góc với ac chứng minh 5 điểm a,d,m,h,e cùng nằm trên một đường tròn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2023
Ta có:AH\(\perp\)BC
=>\(AH\perp\)HM
=>\(\widehat{AHM}=90^0\)
Ta có: \(\widehat{AEM}=\widehat{ADM}=\widehat{AHM}=90^0\)
=>A,E,M,H,D cùng thuộc đường tròn đường kính AH
NT
10 tháng 2 2016
1)Xét tứ giác EMAF có 3 goc vg => AEMF la hcn => các điểm A,E,F,H cùng nằm trên một đường tròn
2)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2023
a. Em tự giải
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
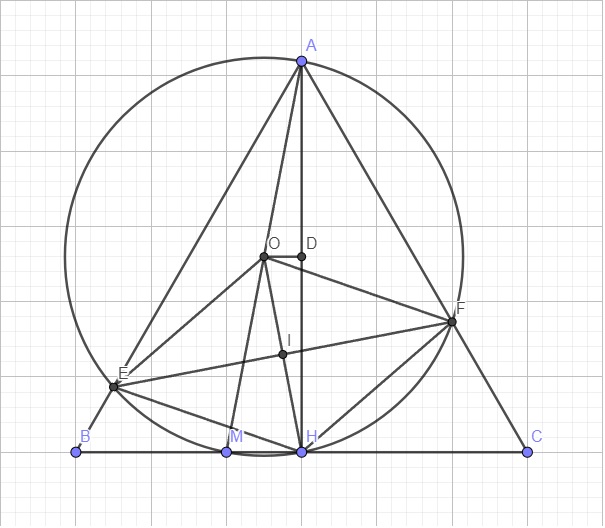
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H
DT
20 tháng 1 2022
hình bạn tự vẽ nhe
a, Xét tứ giác ADME có 3 góc vuông:\(MDA=DAE=MEA=90^o\)
do đó : ADME là hình chữ nhật.
b, Xét tam giác ABC có đường t.b ME (1)
lại có M là trung điểm BC và ME//DA
=> D là trung điểm của AB (2)
từ (1) và (2) suy ra:
\(ME=\dfrac{1}{2}AB\)
hay ME=DB và ME//DB
vậy tứ giác ADME là hình bình hành
c,
Xét tam giác EHD và tam giác EAD có
DE cạnh chung
AD=DH(gt)
góc HED = góc AED (gt)
do đó 2 tam giác EHD và EAD = nhau
=> HE = AE ( 2 cạnh tương ứng )(3)
Xét hình chữ nhật ADME có :
DM= AE ( 2 cạnh đối = nhau )(4)
từ (3) và (4) suy ra :
HE=DM
Xét tứ giác DEMH có :
HE =DM (cmt)
do đó : DEMH là hình thang cân ( 2 đường chéo = nhau ).
20 tháng 1 2022
a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
29 tháng 11 2023
a) Để chứng minh ADME là hình chữ nhật, ta cần chứng minh rằng các cạnh đối diện của nó bằng nhau và các góc trong của nó bằng 90 độ.
Ta có:
- M là trung điểm của BC, nên BM = MC.
- MD vuông góc với AB, nên góc AMD = 90 độ.
- ME vuông góc với AC, nên góc AME = 90 độ.
Vậy ta có BM = MC, góc AMD = góc AME = 90 độ.
Từ đó, ta có thể kết luận rằng ADME là hình chữ nhật với các cạnh đối diện bằng nhau và các góc trong bằng 90 độ.
b) Để chứng minh DBME là hình bình hành, ta cần chứng minh rằng các cạnh đối diện của nó bằng nhau và các góc trong của nó bằng 180 độ.
Ta có:
- M là trung điểm của BC, nên BM = MC.
- MD vuông góc với AB, nên góc AMD = 90 độ.
- ME vuông góc với AC, nên góc AME = 90 độ.
Vậy ta có BM = MC, góc AMD = góc AME = 90 độ.
Từ đó, ta có thể kết luận rằng DBME là hình bình hành với các cạnh đối diện bằng nhau và các góc trong bằng 180 độ.
c) Để chứng minh DEMH là hình thang cân, ta cần chứng minh rằng các cạnh đáy của nó bằng nhau và các góc đáy của nó bằng nhau.
Ta có:
- M là trung điểm của BC, nên BM = MC.
- MD vuông góc với AB, nên góc AMD = 90 độ.
- ME vuông góc với AC, nên góc AME = 90 độ.
- H là giao điểm của đường cao AH và cạnh BC, nên AH vuông góc với BC.
Vậy ta có BM = MC, góc AMD = góc AME = 90 độ và AH vuông góc với BC.
Từ đó, ta có thể kết luận rằng DEMH là hình thang cân với các cạnh đáy bằng nhau và các góc đáy bằng nhau.
Mik ko biết