Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

em tự vẽ hình nha
Gọi O là trung điểm của AM
Vì tam giác AHM vuông tại H có O là trung điểm cạnh huyền AM
=> OH=OA=OM (1)
CMTT: OA=OM=OE (2)
Vì \(\hept{\begin{cases}MD\perp AB\\ME\perp AC\end{cases}\Rightarrow}\hept{\begin{cases}\widehat{MDA}=90^0\\\widehat{MEA}=90^0\end{cases}}\)
Xét tứ giác ADME có:
góc A= góc MDA = góc MEA = 90 độ
=> ADME là hình chữ nhật ( dhnb )
=> 2 đường chéo DE và AM cắt nhau tại trung điểm mỗi đường và DE=AM
Mà O là trung điểm AM
=> O là trung điểm DE
=> OD=OE (3)
Từ (1), (2) và (3) => OD=OE=OA=OM=OH
=> A,D,H,M,F cùng nằm trên 1 đường tròn

a. Em tự giải
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H

1)Xét tứ giác EMAF có 3 goc vg => AEMF la hcn => các điểm A,E,F,H cùng nằm trên một đường tròn
2)

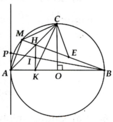
a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)

1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot9}=6\left(cm\right)\)
Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>DE=AH=6(cm)
b: Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=180^0\)
=>ADHE là tứ giác nội tiếp
=>A,D,H,E cùng nằm trên 1 đường tròn
c: \(\widehat{CAK}+\widehat{BAK}=90^0\)
\(\widehat{CKA}+\widehat{HAK}=90^0\)
mà \(\widehat{BAK}=\widehat{HAK}\)
nên \(\widehat{CAK}=\widehat{CKA}\)
=>ΔCAK cân tại C
ΔCAK cân tại C
mà CI là đường trung tuyến
nên CI là đường cao
=>CI vuông góc AK
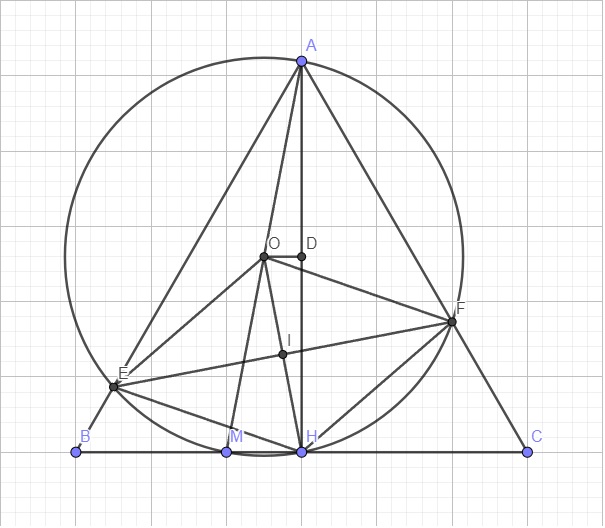
Ta có:AH\(\perp\)BC
=>\(AH\perp\)HM
=>\(\widehat{AHM}=90^0\)
Ta có: \(\widehat{AEM}=\widehat{ADM}=\widehat{AHM}=90^0\)
=>A,E,M,H,D cùng thuộc đường tròn đường kính AH