Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

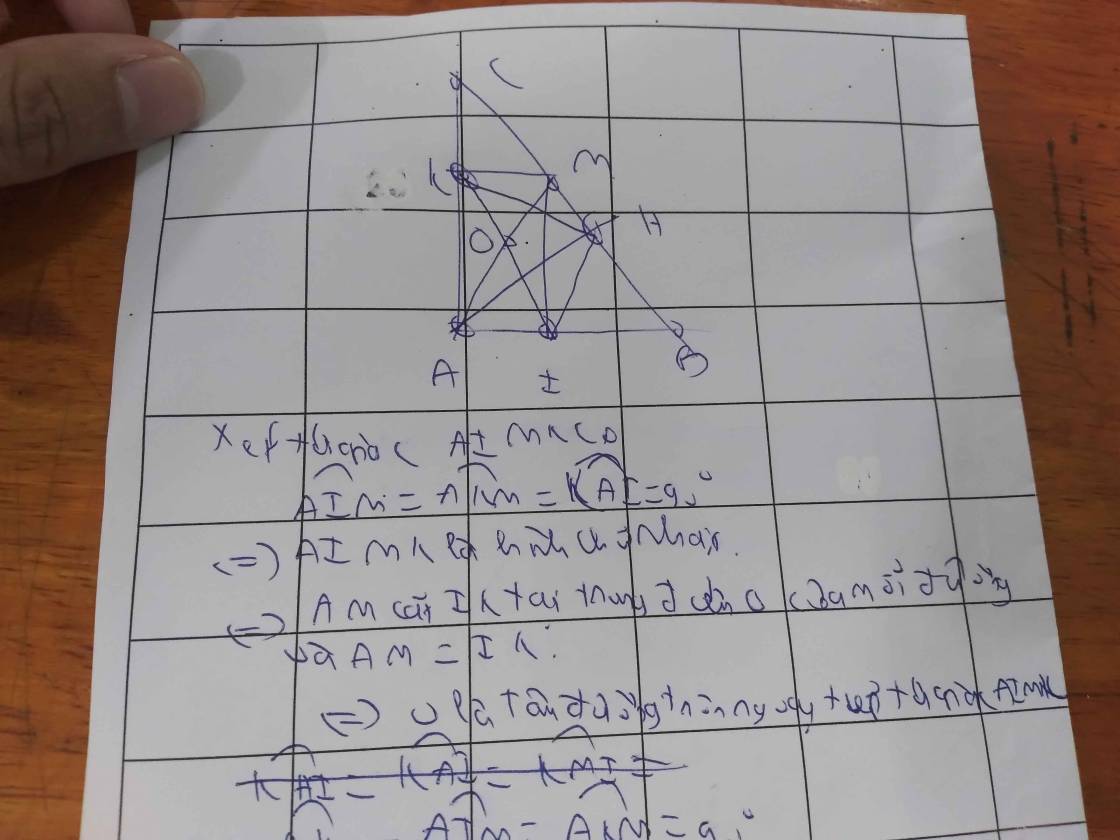
Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
=>AIMK là hình chữ nhật
=>AIMK nội tiếp đường tròn đường kính AM và IK
=>Tâm O của đường tròn ngoại tiếp tứ giác AIMK là trung điểm chung của AM và IK
\(\widehat{AHM}=\widehat{AKM}=\widehat{AIM}=90^0\)
=>A,K,M,H,I cùng thuộc đường tròn đường kính AM
=>H thuộc (O)
Xét (O) có
ΔKHI nội tiếp
KI là đường kính
Do đó: ΔKHI vuông tại H
=>\(\widehat{KHI}=90^0\)

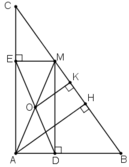
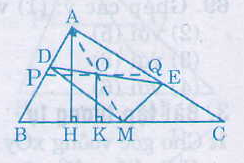
a) Tứ giác ADME có: 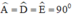
⇒ ADME là hình chữ nhật
O là trung điiểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng.
b) Kẻ AH ⊥ BC; OK ⊥ BC.
Ta có OA = OM, OK // AH (cùng vuông góc BC)
⇒ MK = KH
⇒ OK là đường trung bình của ΔMAH
⇒ OK = AH/2.
⇒ điểm O cách BC một khoảng cố định bằng AH/2
⇒ O nằm trên đường thẳng song song với BC.
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.

Bài giải:
a) Tứ giác ADME có ˆA=ˆD=ˆE=900A^=D^=E^=900
nên ADME là hình chữ nhật
O là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng
b)Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:
Cách 1:
Kẻ OK ⊥ BC. Ta có OA = OM, OK // AH (cùng vuông góc BC).
Suy ra OK=12AHOK=12AH
Điểm O cách đoạn BC cố định một khoảng không đổi bằng 12AH12AH. Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB. Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
Cách 2: Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.
Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.

a) Tứ giác ADME có ˆA=ˆD=ˆE=900A^=D^=E^=900
nên ADME là hình chữ nhật
O là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng
b)Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:
Cách 1:
Kẻ OK ⊥ BC. Ta có OA = OM, OK // AH (cùng vuông góc BC).
Suy ra OK=12AHOK=12AH
Điểm O cách đoạn BC cố định một khoảng không đổi bằng 12AH12AH. Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB. Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
Cách 2: Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.
Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.
=

Hình bạn tự vẽ nha
a) \(\Delta AEM\)vuông tại E có EI là trung tuyến
=> EI = IA (1) => \(\Delta EIA\)cân tại I, có EIM là góc ngoài
=> \(\widehat{EIM}=2\widehat{EAI}\)
Tương tự ta có \(\widehat{HIM}=2\widehat{HAI}\)và IH = IA (2)
Từ (1) và (2) suy ra IE = IH hay \(\Delta EIH\)cân tại I
có \(\widehat{EIH}=\widehat{EIM}+\widehat{HIM}=2\widehat{EAI}+2\widehat{HAI}=2\widehat{EAH}=2\left(90^o-\widehat{ABH}\right)=2\left(90^o-60^o\right)=60^o\)
Vậy EIH là tam giác đều, suy ra EI = EH = IH
Tương tự ta có IHF là tam giác đều, suy ra IH = HF = IF
=> EI = EH = IF = HF
Vậy HEIF là hình thoi
b) \(\Delta ABC\)là tam giac đều nên AH là đường cao cũng là đường trung tuyến
có G là trọng tâm nên \(AG=\frac{2}{3}AH\)(3)
Gọi K là trung điểm AG, suy ra \(AK=KG=\frac{1}{2}AG\)(4)
Từ (3) và (4) suy ra AK = KG = GH
Gọi O là giao điểm của EF và IH, suy ra OI = OH
\(\Delta AMG\)có IK là đường trung bình nên IK // MG
\(\Delta IKH\)có OG là đường trung bình nên IK // OG
=> M, O, G thẳng hàng (tiên đề Ơ-clit)
Vậy EF, MG, HI đồng quy
c) HEIF là hình thoi nên \(EF\perp HI\)
\(\Delta EIH\)đều có EO là đường cao nên \(EO=EI\sqrt{\frac{3}{4}}\)(bạn tự chứng minh)
\(EF=2EO=2EI\sqrt{\frac{3}{4}}=AM\sqrt{\frac{3}{4}}\)(5)
EF đạt GTNN khi AM đạt GTNN
mà \(AM\ge AH\)nên EF đạt GTNN khi M trùng H
Khi đó AM là đường cao trong tam giác đều ABC nên ta cũng có \(AM=AB\sqrt{\frac{3}{4}}=a\sqrt{\frac{3}{4}}\)(6)
Từ (5) và (6) suy ra \(EF=a\left(\sqrt{\frac{3}{4}}\right)^2=\frac{3}{4}a\)
Vậy EF đạt GTNN là \(\frac{3}{4}a\)khi M là chân đường cao hạ từ A xuống BC.
Ở đề không có điểm K, sao ở câu hỏi lại có điểm K vậy em?