a) (3x-2)(4x + 5) = 0
b) (2,3x6,9) (0,1x + 2) = 0
c) (4x + 2)(x² + 1) = 0
d) (2x + 7)(x-5) (5x + 1) = 0
c) 2x(x+3)5(x + 3) = 0
f) (x²-4)(x-2)(3-2x) = 0
g) x³-3x2+3x-1=0
h) x(2x-7) - 4x + 14 = 0
k) (2x-5)²(x + 2)2 = 0
1) x(2x - 9) = 3x(x-5)
m) (x²-2x+1)-4=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c) 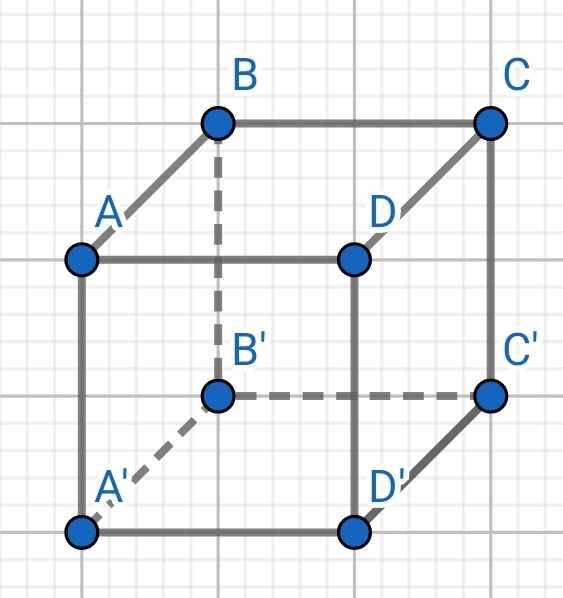
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3

a) \(5x + 3y < 20\)
Đây là bất phương trình bậc nhất hai ẩn.
Chọn \(x = 0;y = 0\)
Khi đó bất phương trình tương đương với 5.0+3.0
Vậy (0;0) là một nghiệm của bất phương trình trên.
b) \(3x - \frac{5}{y} > 2\)
Đây không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.

Đáp án C
Nhắc lại: xác suất của biến cố A được định nghĩa 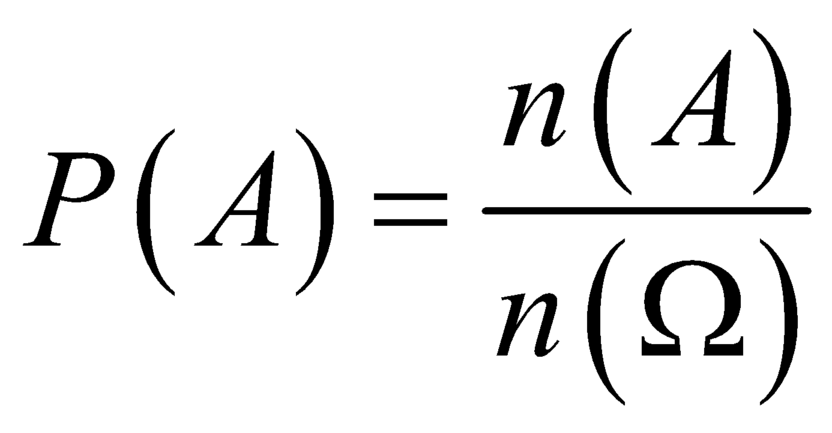 , với
, với ![]() là số phần tử của A,
là số phần tử của A, ![]() là số các kết quả có thể xảy ra của phép thử. Số phần tử của không gian mẫu là
là số các kết quả có thể xảy ra của phép thử. Số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố ![]() , ta có
, ta có
A={(1;1) ;..(1;6); (2;2);..;(2;6);(3;3);..; (3;6); (4;5); (4;6)}
Suy ra ![]() . Vậy xác suất để phương trình bậc hai
. Vậy xác suất để phương trình bậc hai ![]() vô nghiệm là 17/36.
vô nghiệm là 17/36.

a) PT bậc nhất một ẩn là: x-2=0; 4-0,2x=0
b) Giải:
x-2=0 (*)
⟺ x=-2
Vậy tập nghiệm của pt (*) là S={-2}
4-0,2x=0 (**)
⟺-0,2x=-4
⟺x=-4/-0,2=20
Vậy tập nghiệm của pt (**) là S={20}

1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực

\(\orbr{\begin{cases}x-\frac{13}{18}y=0\\x-\frac{18}{13}y=0\end{cases}}\)
\(g.x^3-3x^2+3x-1=0\\ \Leftrightarrow\left(x-1\right)^3=0\\ \Leftrightarrow x-1=0\\ \Leftrightarrow x=1\\ h.x\left(2x-7\right)-4x+14=0\\ \Leftrightarrow x\left(2x-7\right)-2\left(2x-7\right)=0\\ \Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x=7\\x=2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\\ k.\left(2x-5\right)^2\left(x+2\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\\ l.x\left(2x-9\right)=3x\left(x-5\right)\\ \Leftrightarrow3x^2-15x-2x^2+9x=0\\ \Leftrightarrow x^2-6x=0\\ \Leftrightarrow x\left(x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\\ m.\left(x^2-2x+1\right)-4=0\\ \Leftrightarrow\left(x-1\right)^2=2^2\\ \Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2+1=3\\x=-2+1=-1\end{matrix}\right.\)
a: (3x-2)(4x+5)=0
=>\(\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
c: \(\left(4x+2\right)\left(x^2+1\right)=0\)
mà \(x^2+1>=1>0\forall x\)
nên 4x+2=0
=>4x=-2
=>\(x=-\dfrac{1}{2}\)
d: (2x+7)(x-5)(5x+1)=0
=>\(\left[{}\begin{matrix}2x+7=0\\x-5=0\\5x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=5\\x=-\dfrac{1}{5}\end{matrix}\right.\)
f: \(\left(x^2-4\right)\left(x-2\right)\left(3-2x\right)=0\)
=>\(\left(x-2\right)^2\cdot\left(x+2\right)\left(3-2x\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x+2=0\\3-2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)