Giúp mình bài này với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 4 2021
TRẢ LỜI:
Đáp án: C
Trong hiện tượng giao thoa sóng trên mặt nước, khoảng cách giữa hai cực đại liên tiếp nằm trên đường nối tâm hai sóng có độ dài là một nửa bước sóng.
H
20 tháng 8 2023
Xét hình bình hành ABCD có:
\(AB=CD=8\left(cm\right)\)
Đặt độ dài cạnh BC của hình bình hành là x:
\(BC=AD=x\left(cm\right)\)
Chu vi hình bình hành là 30cm:
\(2AB+2BC=30\left(cm\right)\\ \Leftrightarrow2.8+2BC=30\\ \Leftrightarrow BC=\dfrac{30-16}{2}=7\left(cm\right)\)
13 tháng 2 2022
Áp dụng định lý Pi-ta-go ta có:
\(AB^2+AC^2=BC^2\\ \Rightarrow21^2+28^2=BC^2\\ \Rightarrow BC=\sqrt{21^2+28^2}\\ \Rightarrow BC=35\left(cm\right)\)
15 tháng 4 2017
Bạn có thể vẽ hình ra được không? Mình không thể hình dung được bạn à! ~_~
13 tháng 2 2022
Áp dụng định lý Pi-ta-go ta có:
\(NO^2+MO^2=MN^2\\ \Rightarrow MO^2=MN^2-NO^2\\ \Rightarrow MO=\sqrt{55^5-44^2}\\ \Rightarrow MO=33\left(cm\right)\)
13 tháng 3 2017
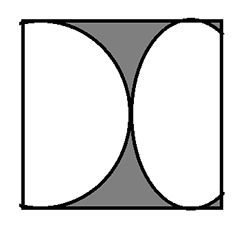
Cạnh hình vuông ABCD là :
4+4 bằng 8 ( cm )
S hình vuông ABCD là :
8x8 bằng 64 ( cm2 )
Vì 1 nửa cạnh hình vuông ABCD bằng bán kính hình tròn nên S hình tròn là :
4x4x3,14 bằng 50,24 ( cm2 )
S phần tô đậm là :
64-50,24 bằng 9,76 ( cm2 )
Đ/S : 9,76 cm2
31 tháng 3 2016
Cho cạnh hình vuông là a, diện tích hình vuông là a x a
Nếu cạnh hình vuông gấp lên hai lần thì diện tích là a x 2 x a x 2 = a x a x 2 x 2 = a x a x 4
=> Diện tích hình vuông gấp lên 4 lần
6 tháng 4 2019
144 = 12 x 12
Vậy cạnh hình vuông có diện tích gấp 2 lần cạnh hình vuông ABCD là : 12 m
Cạnh hình vuông ABCD là :
12 : 2 = 6 ( m )
Cạnh hình vuông cần tích là :
6 x 3 = 18 ( m )
Diện tích hình vuông là :
18 x 18 = 324 ( m\(^2\))
6 tháng 4 2019
Hình vuông có cạnh gấp đôi cạnh hình vuông ABCD sẽ có diện tích gấp 4 lần diện tích hình vuông ABCD
Diện tích hình vuông ABCD là :
144:4=36(m2)
Ta có :36=6x6
Vậy cạnh hình vuông ABCD là 6m
Hình vuông có cạnh gấp 3 lần cạnh hình vuôngABCD có diện tích là
(6x3)x(6x3)=18x18=324(m2)
Đáp số: 324 m2
a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(BF=FC=\dfrac{BC}{2}\)
\(DK=KC=\dfrac{DC}{2}\)
mà AB=BC=CD
nên AE=EB=BF=FC=DK=KC
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
b: Xét ΔDCF vuông tại C và ΔCBE vuông tại B có
DC=CB
CF=BE
Do đó: ΔDCF=ΔCBE
=>\(\widehat{DFC}=\widehat{CEB}\)
mà \(\widehat{CEB}+\widehat{BCE}=90^0\)
nên \(\widehat{BCE}+\widehat{DFC}=90^0\)
=>CE\(\perp\)DF