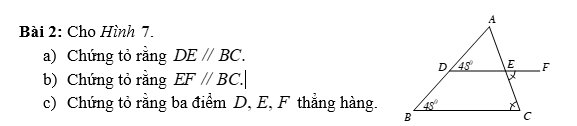
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: MD//AC
=>góc MDB=góc ACB
=>góc MDB=60 độ
Xét tứ giác BEMD có
EM//BD
góc B=góc MDB
=>BEMD là hình thang cân
ME//BC
=>góc AEM=góc ABD=60 độ
Xét tứ giác AEMF có
MF//AE
góc A=góc MEA
=>AEMF là hình thang cân
MF//AE
=>góc CFM=góc CAB=60 độ
Xét tứ giác DCFM có
DM//FC
góc DCF=góc MFC
=>DCFM là hình thang cân
b: Sửa đề: Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của tam giác nào
AEMF là hình thang cân
=>AM=EF
BEMD là hình thang cân
=>BM=ED
FMDC là hình thang cân
=>MC=FD
=>Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của ΔEFD

a: ME//AB
=>góc CEM=góc CAB=60 độ
=>góc CEM=góc C
Xét tứ giác MECD có
MD//EC
góc MEC=góc DCE
=>MECD là hình thang cân
=>góc EMD=180-60=120 độ
MF//BC
=>góc AFM=góc ABC=60 độ
Xét tứ giác AFME có
ME//AF
góc MFA=góc EAF
=>AFME là hình thang cân
=>góc FME=180-60=120 độ
MD//AC
=>góc MDB=góc ACB=60 độ
=>góc MDB=góc B
Xét tứ giác BFMD có
FM//BD
góc B=góc MDB
=>BFMD là hình thang cân
=>góc FMD=180-60=120 độ
=>góc FME=góc FMD=góc DME
b: AEMF là hình thang cân
=>AM=EF
BFMD là hình thang cân
=>BM=FD
MECD là hình thang cân
=>MC=ED
=>MA,MB,MC lần lượt là độ dài 3 cạnh của ΔDEF
=>Trong 3 đoạn MA,MB,MC, đoạn lớn nhất nhỏ hơn tổng 2 đoạn còn lại

a) Để chứng minh gốc EMD = DMF = EMF, ta sẽ sử dụng quan sát về tỷ lệ các đoạn thẳng song song trong tam giác, cụ thể là định lý Thales. Theo định lý Thales, khi có hai đường thẳng song song cắt các đường thẳng chéo khác, các đoạn thẳng chéo tương ứng cắt bởi hai đường thẳng song song này có tỷ lệ đồng nhất. Áp dụng định lý Thales, ta chứng minh: - Ta có đường thẳng song song qua M và song song AC cắt BC tại D, suy ra MD // AC. - Ta cũng có đường thẳng song song qua M và song song với AB cắt AC tại E, suy ra ME // AB. Từ đây, ta có thể suy ra góc tức thời EMD = DMF = 180° - góc MEF (do cặp góc đối nhau). Tiếp theo, ta cần chứng minh góc MEF = góc EMF. - Ta biết rằng EM // AB (vì đường thẳng EM song song với AB). - Vì tam giác ABC đều nên mọi cặp góc tại đỉnh của tam giác đều bằng nhau. Do đó, góc AEC = góc ACE. - Từ hai đường thẳng song song EM và AB và hai cặp góc bằng nhau AEC = ACE, ta suy ra hai góc AME = CMB. - Ngược góc AMF = CMB (vì AM // BC) nên suy ra AME = AMF. Kết hợp với công thức trên, ta có: góc MEF = góc EMF. Từ cả hai phần trên, ta kết luận được đặt ở góc độ EMD = DMF = EMF. b) Để chứng minh rằng trong 3 đoạn MA, MB, MC, đoạn lớn nhất nhỏ hơn tổng hai đoạn kia, ta có thể áp dụng quy tắc tam giác: - Giả sử MA > MB và MA > MC. - Ta cần chứng minh MA < MB + MC. - Ta có thể viết MA = MB + x và MA = MC + y, trong đó x và y là độ dài của hai đoạn thẳng MB và MC so với đoạn MA. - Từ giả thuyết, x > 0 và y > 0. - Khi đó, MB = MA – x và MC = MA – y. - Đặt nay xem xét tổng MB + MC = (MA – x) + (MA – y) = 2MA – (x + y). - Vì x > 0 và y > 0 nên x + y > 0. - Như vậy, tổng MB + MC < 2MA, suy ra MA < MB + MC. - Do đó, trong 3 đoạn MA, MB, MC, đoạn lớn nhất nhỏ hơn tổng hai đoạn kia. Do đó, ta đã chứng minh được cả hai phần a và b.

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.
a) Ta có:
\(\widehat{ADE}=\widehat{ABC}\left(=45^o\right)\)
Mà hai góc này ở vị trí đồng vị
=> DE//BC
b) Ta có:
\(\widehat{FEC}=\widehat{ECB}\left(gt\right)\)
Mà hai góc này ở vị trí so le trong
=> EF//BC
c) Ta có: DE//BC
=> \(\widehat{DEC}+\widehat{ECB}=180^o\) (trong cùng phía)
Mà: \(\widehat{FEC}=\widehat{ECB}\left(gt\right)\)
\(=>\widehat{FEC}+\widehat{ECB}=180^o\)
\(=>\widehat{DEF}\) là góc bẹt
=> D, E, F thẳng hàng