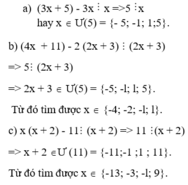Tìm a sao cho: 2x mũ 3-3x mũ2 + x+ a chia hết cho x+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2020
a) Ta có :
\(x^2-2x+1=6y^2-2x+2\)
\(\Leftrightarrow x^2=6y^2+1\)
\(\Leftrightarrow x^2-1=6y^2\)
Mà \(6y^2⋮2\)
\(\Leftrightarrow6y^2=\left(x-1\right)\left(x+1\right)⋮2\)
Mặt khác : \(\left(x-1\right)+\left(x+1\right)=2x⋮2\)
\(\Leftrightarrow x-1;x+1\)cùng chẵn
\(\Rightarrow x-1;x+1\)là hai số chẵn liên tiếp
\(\Rightarrow\left(x-1\right)\left(x+1\right)⋮8\)
\(\Leftrightarrow6y^2⋮8\)
\(\Leftrightarrow3y^2⋮4\)
\(\Leftrightarrow y^2⋮4\)
\(\Leftrightarrow y⋮2\)
Do \(y\in P\):
\(\Rightarrow y=2\)
\(\Rightarrow x=5\)
Vậy........
b) Xét hiệu : \(A=9\left(7x+4y\right)-2\left(13x+18y\right)\)
\(\Rightarrow A=63x+36y-26x-36y\)
\(\Rightarrow A=37x\)
\(\Rightarrow A⋮37\)
Vì \(7x+4y⋮37\)
\(\Rightarrow9\left(7x+4y\right)⋮37\)
Mà \(A⋮37\)
\(\Rightarrow2\left(13x+18y\right)⋮37\)
Do 2 và 37 nguyên tố cùng nhau :
\(\Rightarrow13x+18y⋮37\)
Vậy...................
2 tháng 8 2021
Bài 1:
a) Ta có: \(\left(2x-1\right)^{20}=\left(2x-1\right)^{18}\)
\(\Leftrightarrow\left(2x-1\right)^{20}-\left(2x-1\right)^{18}=0\)
\(\Leftrightarrow\left(2x-1\right)^{18}\left[\left(2x-1\right)^2-1\right]=0\)
\(\Leftrightarrow\left(2x-1\right)^{18}\cdot\left(2x-2\right)\cdot2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=1\end{matrix}\right.\)
b) Ta có: \(\left(2x-3\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
c) Ta có: \(\left(x-5\right)^2=\left(1-3x\right)^2\)
\(\Leftrightarrow\left(x-5\right)^2-\left(3x-1\right)^2=0\)
\(\Leftrightarrow\left(x-5-3x+1\right)\left(x-5+3x-1\right)=0\)
\(\Leftrightarrow\left(-2x-4\right)\left(4x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)
2 tháng 8 2021
Bài 2:
a) \(15^{20}-15^{19}=15^{19}\left(15-1\right)=15^{19}\cdot14⋮14\)
b) \(3^{20}+3^{21}+3^{22}=3^{20}\left(1+3+3^2\right)=3^{20}\cdot13⋮13\)
c) \(3+3^2+3^3+...+3^{2007}\)
\(=3\left(1+3+3^2\right)+...+3^{2005}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{2005}\right)⋮13\)
24 tháng 1 2021
a, \(3x-8⋮x-4\)
\(3\left(x-4\right)+4⋮x-4\)
\(4⋮x-4\)hay \(x-4\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| x - 4 | 1 | -1 | 2 | -2 | 4 | -4 |
| x | 5 | 3 | 6 | 2 | 8 | 0 |
c, tương tự
24 tháng 1 2021
a,Gợi ý:vì x^2+x+1 chia hết cho x+1 => x^2 chia hết cho x+1 b,Gợi ý nhân 3 với (x-4) rồi lấy 3x-8 trừ đi c,lấy (x+5) trừ đi x-2 e,Gợi ý x^2+2x-7 chia hết cho x+2
17 tháng 11 2020
a) x chia hết cho 15, =) x=B(15)
B(15)={0;15;30;45;60;75;...}
mà x bé hơn hoặc bằng 60 nên x ={0;15;30;45;60}
17 tháng 11 2020
c) vì 180 chia hết cho x,150 chia hết cho x,84 chia hết cho x,x lớn nhất =) x=ƯCLN(180,150,84)
ƯCLN(180,150,84)
180=2mũ2 . 3mũ2 . 5
150=2 . 3 . 5mũ2
84=2mũ2 . 3 . 7
ƯCLN(180,150,84)=6
TT
0
CM
13 tháng 6 2019
a) (3x + 5) - 3x chia hết cho x =>5 chia hết cho x hay x Î Ư(5) = {- 5; -1; 1;5}.
b) (4x + 11) - 2 (2x + 3) chia hết cho (2x + 3) => 5 chia hết cho (2x + 3)
=> 2x + 3 Î Ư(5) = {-5; -l; l; 5}. Từ đó tìm được x Î {-4; -2; -l; l}.
c) x (x + 2) - 11chia hết cho (x + 2) => 11 chia hết cho (x + 2)
=> x + 2 ÎƯ (11) = {-11;-1 ;1 ; 11}.
Từ đó tìm được x Î {-13; -3; -l; 9}.